Shadow Rendering 阴影绘制方法的发展过程

课程名称：计算机图形学（研究生）
报告主题：图形处理器(GPU)的历史、现状和展望
提交日期：2023 年 1 月 1 日

渲染技术研究报告——阴影绘制技术的发展历程及方法比较

一、前言

阴影绘制是真实感渲染中非常重要的一个模块，对提高场景的真实度有着至关重要的作用，不管是使用光栅化的流程还是光线追踪的流程进行场景绘制，阴影绘制的技术都经过了多次的更新和迭代。我也在一些课程中学习过一些简单的阴影绘制方法，因此想借此机会对所有的阴影绘制方法做一个系统性的梳理和总结。阴影绘制的方法按照时间发展顺序主要有Shadow Volume算法、Shadow Map算法、PCF算法、PCSS算法、VSM算法等等。

首先，阴影的定义是Shadow is the region of space for which at least on point of the light source is occluded，也就是绘制中那些至少对一盏光源，其没有被直接照亮而是被其他物体遮挡住的区域。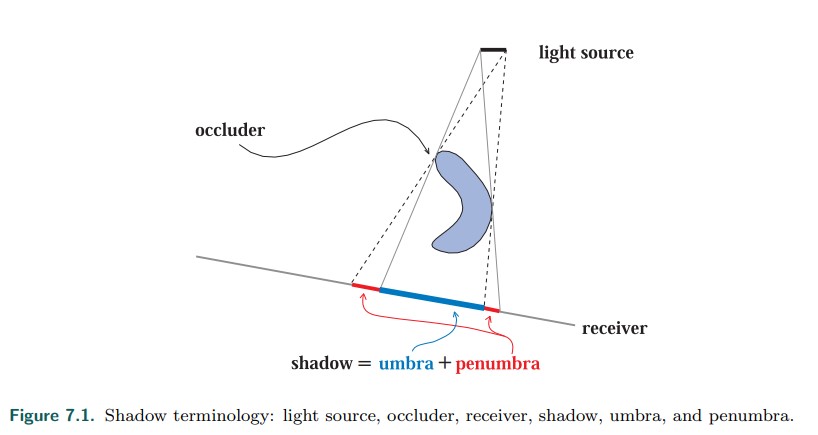


图源Real-Time Rendering 4th
如上图所示，要实现阴影的绘制，需要考虑的有光源、遮挡物（Occluder）、接受物（Receiver）、本影区（umbra）半影区（penumbra）等。

其中，对于接收物体是平面的情况，我们可以直接通过光源位置、物体几何等信息进行光线求交几何计算，解析地得到平面上阴影的形状和范围（如下图），但是这显然无法处理复杂的场景阴影绘制，也不是我们需要的通用的方法，也因此本文仍然选择聚焦于在任何曲面或者几何体上产生阴影的通用方法。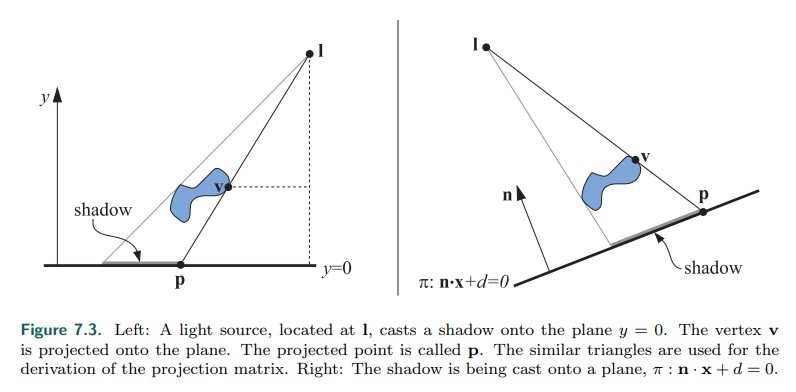


图源Real-Time Rendering 4th

二、Shadow Volume算法诞生及其改进

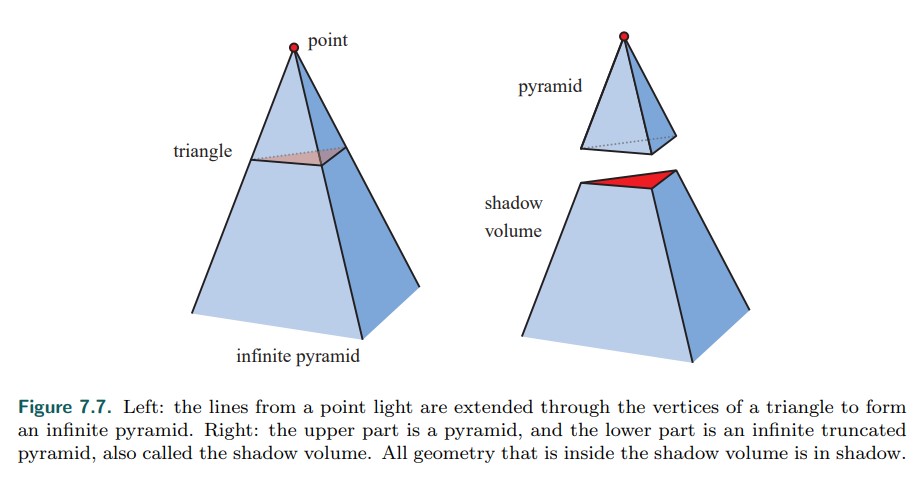
图源Real-Time Rendering 4th
Shadow Volume是Franklin在1977年提出的阴影绘制算法，虽然在今天这个算法由于其较大的开销已经不太被使用，但我们仍然可以从中学到一些基础的思维方式，并且由于该算法不是在图像空间进行的，因此不会像Shadow Map一样收到采样的影响。

Shadow Volume算法的基本思想是对于投影物体（以一个三角形为例），以光源为出发点建立一个类似金字塔的无限延伸的体积结构，并切除在光源点和投影物体之间的部分。所有包含在剩余体积范围内的区域都处在阴影中。

对于场景中的所有物体，都可以使用该方法建立其投影金字塔。在正常绘制场景时，对于每一哥Fragment，都需要遍历所有的投影金字塔，计算其是否被包含在其中并记录被包含的次数。被包含的越多，则该处阴影强度越大（阴影颜色更暗）。以此类推，绘制完成所有的Fragment。可想而知，对于较为复杂的场景，Shadow Volume方法需要的时间和空间开销都是巨大的，不仅需要管理每一个投影物体的投影金字塔，还需要对任何一个片元进行所有金字塔的遍历测试。如果场景中包含N个物体，且都可以投射阴影，则该算法的时间复杂度将达到O(n²)。

三、Shadow Map算法的诞生及其改进

早在 1968年，Arthur Appel就在研究隐藏面消除时提出了光线投射算法（Ray Casting），并首次给出了光线跟踪算法的描述。其具体思路是从每一个像素射出一条射线，然后找到最接近的物体挡住射线的路径，而视平面上每个像素的颜色取决于从可见光表面产生的亮度。

1974年，Catmull为了解决消隐问题提出了Z-Buffer算法，该算法的主要思路是使用一个屏幕空间的缓存，记录每一个像素点所对应的最小深度，在绘制每一个多边形时，与对应像素位置的当前最小深度做对比，如果小于该值则证明该多边形可见，绘制并更新Z-Buffer。Z-Buffer算法思路简单且通用性较好，为之后图形学的许多技术提供了理论基础。

因此在1978年，William以Z-Buffer算法为基础，提出了Shadow Map算法，主要思想就是维护一个从光源看出的Z-Buffer（也就是Shadow Map）。能从光源出发直接看到的区域就不属于阴影，否则属于阴影。


图源【3】
Shadow Map是一个2-pass的算法。算法主要步骤为：

1. 第一个pass：以光源为视点出发绘制场景，只需要绘制深度信息，像Z-Buffer算法一样记录屏幕空间上每一个像素点的最小深度，得到 Shadow Map。
2. 第二个Pass：正常绘制场景。

• 在每个像素绘制时通过坐标转换，计算出其在光源坐标系下对应的屏幕坐标。
• 如果其在光源坐标系下的深度在浮点数精度下小于等于Shadow Map上对应位置的当前值，则证明该点被光源直接照亮，否则证明该点在阴影中。
  其中，需要做的坐标转换为：首先根据片元当前的屏幕坐标，乘以当前相机投影矩阵的逆矩阵得到其世界坐标，再根据光源坐标系下的投影矩阵计算出在Shadow Map的屏幕坐标。其中，对于太阳光这样的平行光我们需要使用平行投影方式绘制Shadow Map，而对于点光源则应该使用透视投影绘制Shadow Map。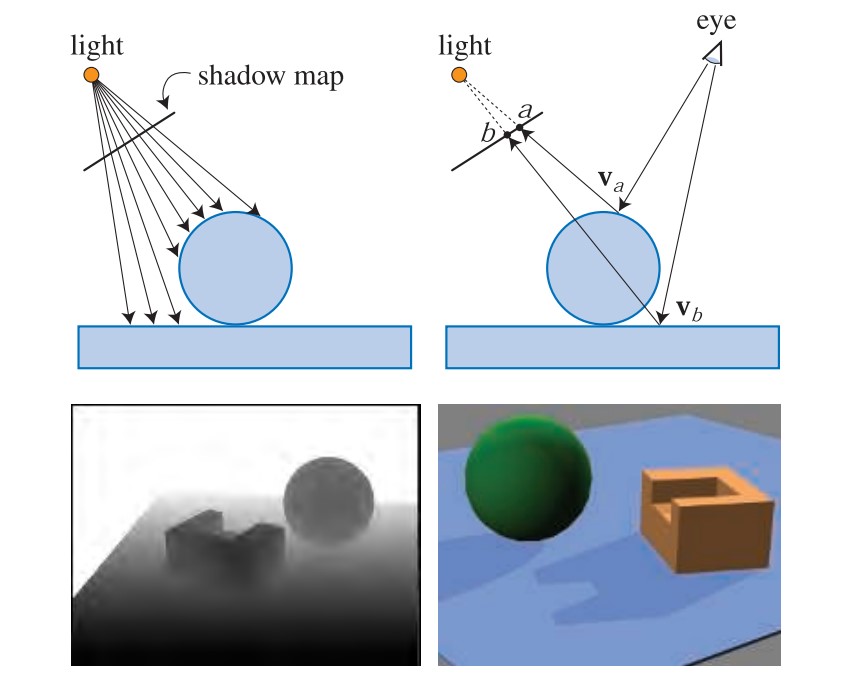
  
  
  图源Real-Time Rendering 4th

不难想到，如何选择Shadow Map绘制的视口是一个至关重要的问题，如果光源坐标系下的视口刚好可以包含正常绘制时所有能看到的物体，如上图中所示，则算法可行，否则可能会出现正常绘制时的某些Fragment对应的光源坐标系下的坐标超过视口范围，在Shadow Map上没有对应点，无法判断是否属于阴影的情况。另外，对于在场景中间的点光源（在不同方向上都可能投射阴影），则一般选择使用一个six-view cude，分别绘制不同方向上的Shadow Map。但这样的解决方法同样也带来了不同view交界处的走样问题。

Shadow Map算法的效果很大程度上受限于 Shadow Map的分辨率，因此在绘制Shadow Map时进行场景物体的剔除和剪枝也是十分有必要的，对于那些在相机中不可见的物体，在Shadow Map中也不需要绘制，这样可以有效缩小Shadow Map绘制的范围，从而对同样分辨率的Shadow Map达到更高的利用率和绘制精度。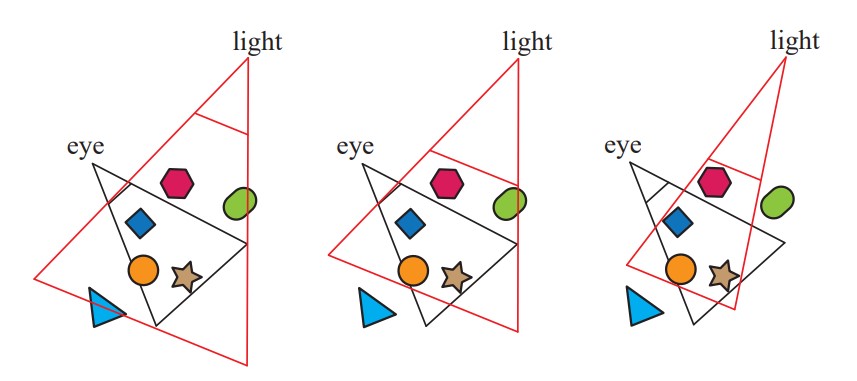


图源Real-Time Rendering 4th

但是普通的Shadow Map算法不可避免地存在着问题，主要的两个问题有自遮挡问题（“surface acne”）和锯齿状走样问题。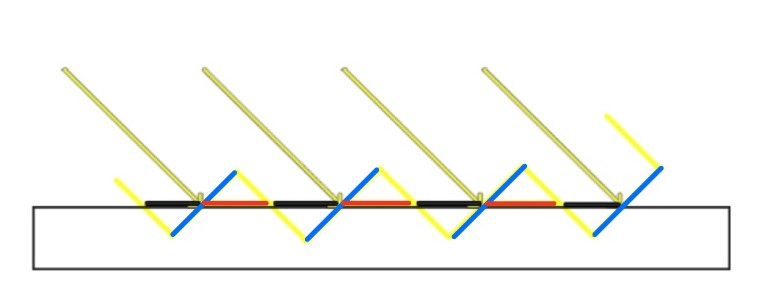


图源网络

其中，自遮挡问题产生的原因是如下图，在从灯光出发进行Shadow Map绘制时，视线方向与接收投影的平面方向存在夹角，但是绘制时仅采样了像素中心的深度值作为整体的深度值。在第二个pass比较深度是就会出现本来同一平面但是有部分像素通不过Shadow Map的深度测试这种情况，从而导致如下图所示的阴影错误。对该问题可以使用设置比较的bias来尝试解决，但是bias过小时不能完全避免这种错误的产生，过大时又会产生如下图中右边所示的阴影和物体不贴合的错误（被称为Light Leaks 或者 Peter Panning），出现物体悬浮的绘制效果。


图源Real-Time Rendering 4th

另外一个解决Self-shadowing自遮挡问题的思路是修改绘制Shadow Map的过程，比如说绘制时进行面剔除（Face Culling），仅绘制模型的背面。这种方法在物体都是流形时（拥有背面和反面）效果较好，能很好地避免surface acne问题。但是无法处理某些模型只有单个面的情况。一种沿着这个思路的改进方法是Second-depth Shadow Map，是在绘制Shadow Map时选择front face和back face的中间值作为Shadow Map的采样值。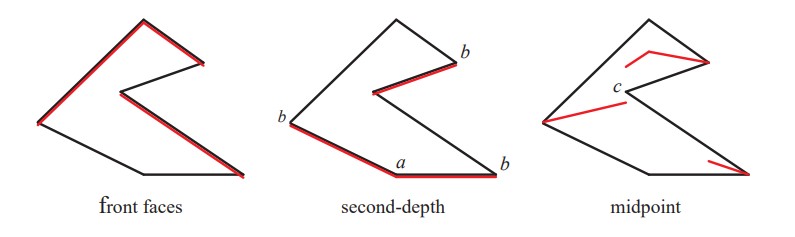


图源Real-Time Rendering 4th

而另一个问题锯齿状走样本质上还是由于Shadow Map的分辨率限制导致的，由于Shadow Map的绘制视口与相机绘制视口不同，可能会导致在相机坐标系下占很大部分的空间在Shadow Map中仅仅对应几个像素，因而导致其不能完全表达出该部分的相互遮挡信息，正常绘制时的较大区域可能整体无法通过Shadow Map的深度测试，产生锯齿状走样。

为了解决分辨率不够导致的锯齿状走样问题，Nvdia提出了CSM算法（Cascaded Shadow Maps），也就是使用级联的阴影贴图。其主要思想就是通过物体的距离，动态地进行不同分辨率的Shadow Map的绘制，比如说对远处的物体采用分辨率较小的Shadow Map，而对于较近处的物体则采用分辨率较大Shadow Map。LearnOpenGL中提供了一种基本的思路：

首先使用相机的视图和投影矩阵，反向计算出它所定义的视锥体在世界坐标系下的位置，然后将其划分为 n 个子视锥体，其中第i个截锥体的远平面是第i+1个截锥体的近平面。然后对于每一个截锥体中的物体依次渲染一张Shadow Map，在正常绘制时，则同样根据Fragment的Z值计算其应该属于哪一个截锥体，从而选取不同的Shadow Map。

需要注意的一点是，如果某个物体不在相机视锥体内，但在光源和某个截锥体之间，则绘制Shadow Map时也需要对其进行考虑，否则也会造成阴影绘制的错误。

四、PCF算法&PCSS算法

普通的Shadow Map只能得到非零即一的阴影测试值，只能绘制硬阴影，这显然不能满足我们真实感渲染的需求，因此在1987年，William T. Reeves引入了本来用于做抗锯齿的PCF算法（Percentage Closer Filter）到阴影绘制领域，在此基础上改良得到Shadow Map算法得到了PCSS算法。

该算法的基本思想是对深度测试的结果进行Filter（而不是直接对Shadow Map进行filter）。具体操作方法是：在第二个Pass进行正常绘制时，对于每一个Fragment的深度测试，不仅比较直接对应的Shadow Map像素，还要与其邻域内（比如说3*3）像素进行深度测试，小于等于（表示不在阴影中）则记为0，大于则记为1，得到一个01的矩阵，对其求平均得到一个0-1之间的浮点数值，则代表该像素的阴影值，这样就能实现软阴影的效果。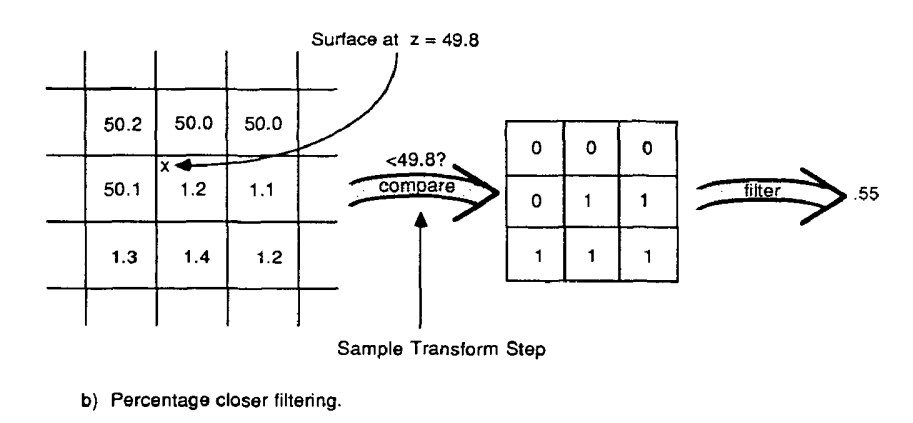


图源【7】
在以上这种思想的指导下我们不难发现，filter的邻域大小一定程度决定了得到的阴影边缘的平滑程度，也就是邻域越大越容易得到“软”阴影。而在生活中，当投影物体靠近接收物体时，我们得到的阴影边缘更硬，反之则较软。以此为指导，Fernando在2005年提出的PCSS算法是在PCF进行阴影绘制基础上的进一步改进。其主要思想是使用如下图所示的几何关系来估计半影区（Penumbra）的宽度（也就是阴影的软硬程度）。其中$d_blocker$指的是投影物体的深度也就是Shadow Map中储存的深度，$d_receiver$指的是接收物体的深度也就是当前片元的深度。而用此方法计算出的半影区的宽度可以指导我们进行PCF中filter邻域大小的选择。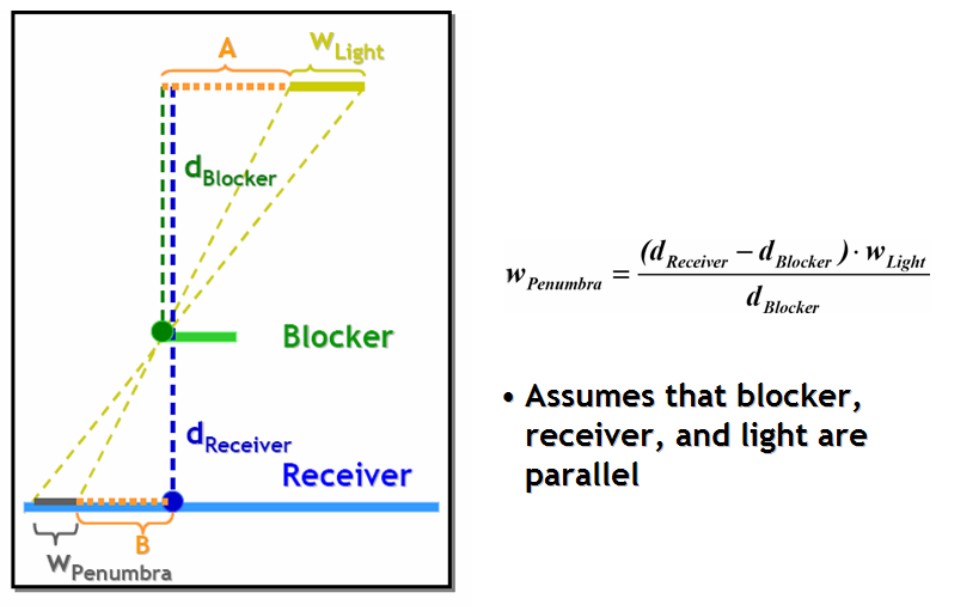


图源【8】

PCSS算法的主要流程为：

1. Blocker Search

• 在一个小的邻域内采样得到投影物体的平均深度。

2. Penumbra Estimation

• 根据投影物体的平均深度和当前片元的深度计算半影区的宽度。

3. Percentage Closer Filtering

• 根据计算出的半影区的宽度选定filter的邻域大小并进行PCF计算。
  其中，在第一步进行投影物体深度的采样时，采样区域的大小可以用下图所示的这种方式选定，也就是根据投影物体的深度和光源的大小计算选定。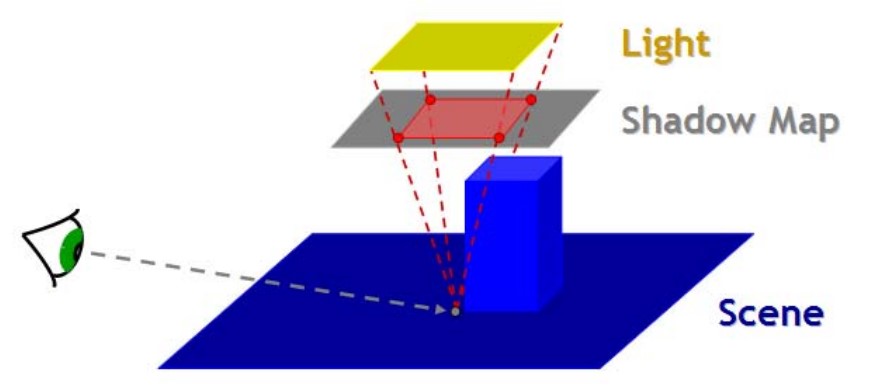
  
  图源【8】

五、VSM算法和VSSM算法

VSM算法全称为Variance Shadow Mapping，VSSM算法全称为Variance Soft Shadow Mapping，这两种算法相互承袭，是一种使用统计学知识对PCSS算法的改进方案，其主要的思路是通过对Shadow Map中Block内的深度分布进行统计学估计，避免大量采样计算PCF的过程，从而加快阴影绘制速度。

PCF算法的基本思想就是在某一个邻域内测试有百分之多少的像素能使得当前片元通过深度测试。也就是测试当前片元的深度在该邻域内分布在百分之多少。VSSM算法引入了统计学的知识，假设当前邻域内的深度分布符合高斯分布，如果要测试当前片元的深度在该邻域内分布在百分之多少，只需要知道当前分布的均值和方差。

对于深度图邻域内均值的计算，我们可以自然地联想到对Shadow Map进行Mipmap查询。而对于方差的计算，VSM引入了以下的公式，因此我们只需要在绘制Shadow Map的同时绘制一个储存深度的平方的map。

$var(x)=E(x^2),-E^2(x)$

这样在Shadow Map绘制完成后，对于其上的每一个点我们都能通过均值和方差得到该位置的一个深度的近似分布情况，从而可以根据当前片元的值，计算出其CDF。另外，VSM算法还引入了切比雪夫不等式（如下），只需要知道分布的期望和方差，就可以计算出x大于某个固定值的概率。

$P(x>t)≤σ^2/(σ^2+(t-μ)^2)$

切比雪夫不等式成立的条件是$t＞μ$，也就是当前的$d＞z_avg$。也就说如果Block内的平均深度小于当前Fragment的深度，就不能使用这种估计方法。

上面这种从统计学出发的估计解决了PCSS算法中的第三个步骤也就是PCF计算，但是PCSS算法中的第一个步骤Blocker Search仍然会耗费较长的时间，因此VSSM算法针对性地提出了估计方案。

对于一个Block，第一个步骤Block Search的目标是估计其中遮挡物的平均深度，我们可以设Block中的像素总数为N，平均深度为$Z_avg$，深度小于当前值（遮挡物）的像素数为N1，平均深度为$Z_occ$，深度大于当前值（接收物体）的像素数为N2，平均深度为$Z_unocc$。则可以得到等式：

$N_1/N Z_unocc+N_2/N Z_occ=Z_avg$

不难看出，N_1/N就是非遮挡物所占比例，也就可以转化为P（X≥t）。则上式可以转化为：

$P(x≥t) z_unocc+(1.0-P(x≥t)) z_occ=z_avg$

要计算遮挡物的平均深度，可以使用：

$Z_occ=(z_avg-P(x≥t) z_unocc)/(1.0-P(x≥t))$

而其中的$Z_avg$可以通过Mipmap得到，因此VSSM假设非遮挡物的深度都是t，从而可以计算出遮挡物的平均深度，这种假设的理论依据是一般的接收物体都是一个平面。而对于那些不是一个平面的阴影接收物体，以及切比雪夫不成立的情况，VSSM这篇论文则提出了分治的解决方案。对不满足$d>z_avg$的Block，将其分割为更小的sub-Block，再进行阴影的绘制计算。

具体的分治思路是，对于那些$z_avg＜d$的sub-Block，我们之前使用切比雪夫不等式的估计仍然是有效的，但是对于那些$z_avg≥d$的sub-Block，论文中选择了直接使用普通的PCSS算法进行阴影的绘制。其原因是论文认为分治之后的sub-Block较小，可以使用传统的PCF采样进行计算。论文使用类似四叉树的结构进行分治之后Block的管理和遍历。

六、MSM算法

MSM算法全称为Moment Shadow Mapping。是Christoph Peters在2015年提出的一种阴影绘制方式。

MSM实际上是在VSSM算法的基础上，对使用统计学思想逼近Depth Map的分布进行阴影绘制这种想法的延续。VSSM算法中，仅仅使用到了Depth的平均值和方差（也就是一阶矩和二阶矩）去估计深度的分布情况，这显然是可能产生偏差的，比如说对于下图中右边这种深度的分布，集中分布在几个固定的值附近，这样的情况使用切比雪夫不等式去估计就会出现比较大的误差。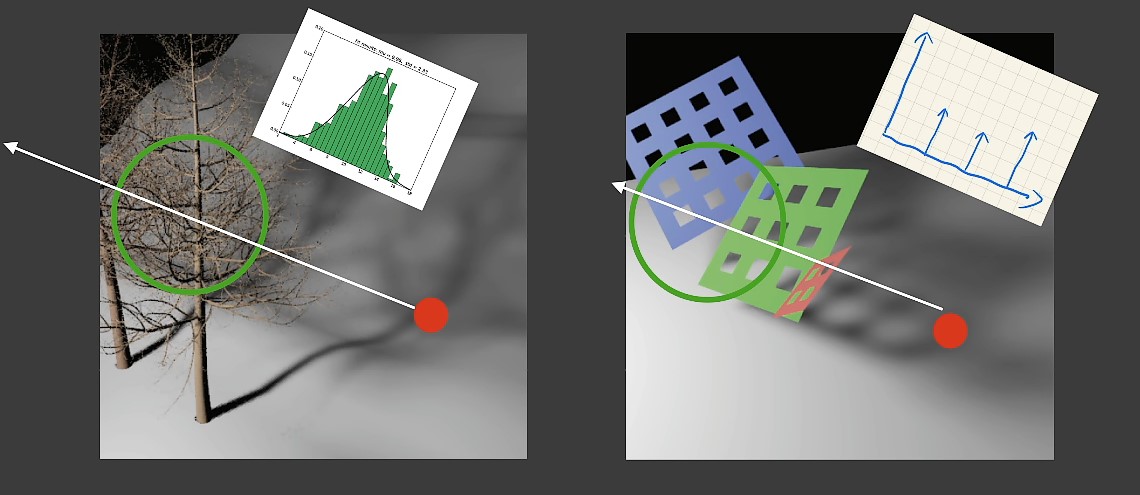


图源Games202
而为了让VSM中对分布的描述更加精确，Christoph Peters提出了使用高阶矩来描述分布的方法。如下图，蓝色表示真正的深度分布CDF，如果使用VSSM算法则只能对CDF逼近到红色线条的程度，而如果使用前四阶矩则能逼近到绿色线段的程度，这样能使得我们对深度分布的估计更精确，对PCF进行近似计算也就更精确。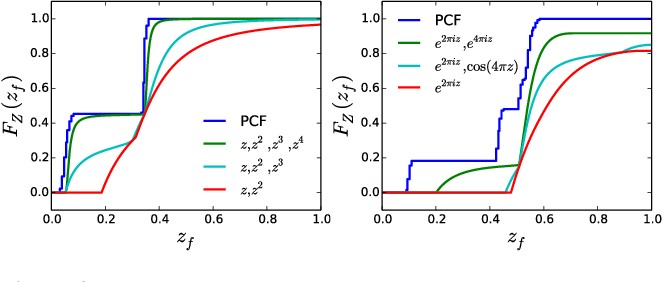


图源【13】
Christoph的测试表明，相对于VSM和ESM算法，MSM算法能提供更小的Shadow绘制误差（如下图）。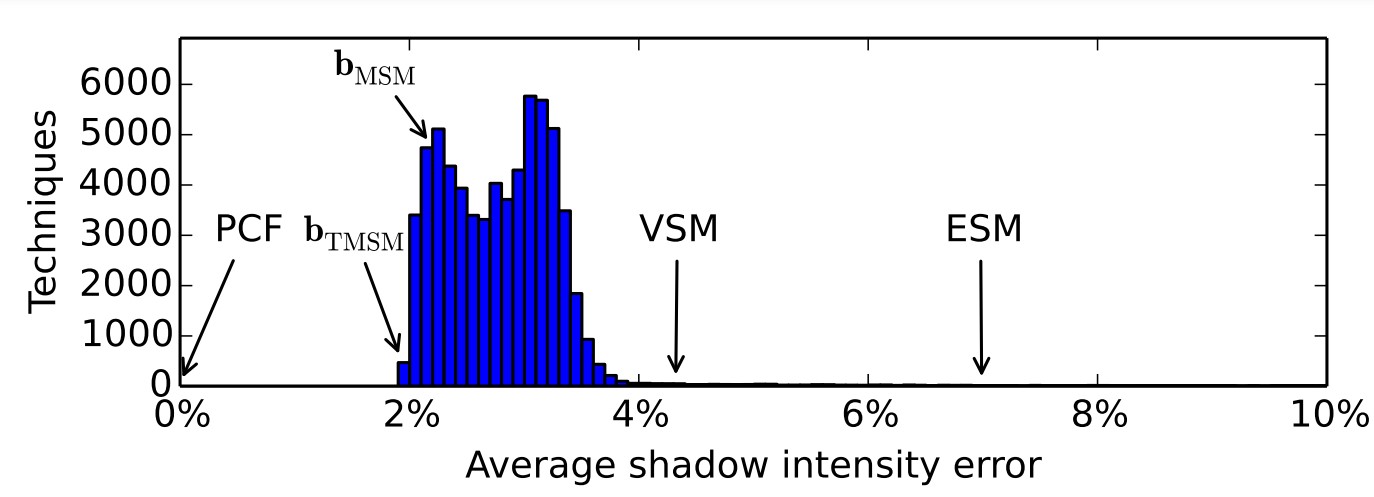


图源【13】

七、总结

在当前的渲染领域，由于时序上降噪技术的引入，实时的光线追踪技术成为了可能，因此目前传统的阴影绘制方法或许没有像之前那样应用这么广泛，但是在顺着这条发展路径学习的过程中，我对渲染的一些理解仍然能加深，并且获得新的启发。传统渲染方式虽然在一定程度上是某个时代算力限制的产物，但是其中蕴含的思考方式和优化方法，相信仍然能在未来的学习中给我带来灵感和启发。

参考资料：

1. Tomas Akenine-Möller, Eric Haines, Naty Hoffman, Angelo Pesce, Michał Iwanicki, and Sébastien Hillaire,T. Real-Time Rendering 4rd Edition[M]. Natick, MA, USA: A. K. Peters, Ltd., 2020.
2. Catmull, E., “A Subdivision Algorithm for Computer Display of Curved Surfaces,” PhD. thesis, Dept. of Computer Science, University of Utah, 1974.
3. Lance Williams. 1978. Casting curved shadows on curved surfaces. SIGGRAPH Comput. Graph. 12, 3 (August 1978), 270–274. https://doi.org/10.1145/965139.807402
4. Y. Wang and S. Molnar. Second-depth shadow mapping. Technical Report TR94-019, Department of Computer Science, University of North Carolina - Chapel Hill, Dec. 1994.
5. Fernando, S. Fernandez, K. Bala, and D. P. Greenberg. Adaptive shadow maps. In SIGGRAPH 2001 Conference Proceedings, pages 387–390, 2001.
6. M. Stamminger and G. Drettakis. Perspective shadow maps. ACM Transactions on Graphics, 21(3):557–562, July 2002.
7. William T. Reeves, David H. Salesin, and Robert L. Cook. 1987. Rendering antialiased shadows with depth maps. SIGGRAPH Comput. Graph. 21, 4 (July 1987), 283–291. https://doi.org/10.1145/37402.37435
8. https://developer.download.nvidia.com/shaderlibrary/docs/shadow_PCSS.pdf
9. William Donnelly and Andrew Lauritzen. 2006. Variance shadow maps. In Proceedings of the 2006 symposium on Interactive 3D graphics and games (I3D ‘06). Association for Computing Machinery, New York, NY, USA, 161–165. https://doi.org/10.1145/1111411.1111440
10. https://developer.download.nvidia.com/SDK/10.5/opengl/src/cascaded_shadow_maps/doc/cascaded_shadow_maps.pdf
11. Salvi, Marco, “Rendering Filtered Shadows with Exponential Shadow Maps,” in Wolfgang Engel, ed., ShaderX6, Charles River Media, pp. 257–274, 2008.
12. Yang, B., Dong, Z., Feng, J., Seidel, H.-P. and Kautz, J. (2010), Variance Soft Shadow Mapping. Computer Graphics Forum, 29: 2127-2134. https://doi.org/10.1111/j.1467-8659.2010.01800.x
13. Christoph Peters and Reinhard Klein. 2015. Moment shadow mapping. In Proceedings of the 19th Symposium on Interactive 3D Graphics and Games (i3D ‘15). Association for Computing Machinery, New York, NY, USA, 7–14. https://doi.org/10.1145/2699276.2699277
14. Lingqi Yan. Games202 Lecture3&Lecture4.
15. https://zhuanlan.zhihu.com/p/384446688
16. https://zhuanlan.zhihu.com/p/478472753