课程名称:计算机动画
一、 实验目的和要求
关键帧动画技术是计算机动画中的一类重要技术。本实验选取线性插值和矢量线性插值作为实验内容,旨在了解关键帧动画系统的结构,变形算法的思想以及不同算法对应的不同性能。
本实验要求实现线性插值和矢量线性插值两种关键帧插值算法的图形化界面展示,用户通过鼠标点击交互选定起点帧和终点帧的关键点,由程序自行生成起始帧的图形,并且通过计算得到中间的插值图像,连续播放形成关键帧动画。
二、 实验内容和原理 系统包括三个部分:
输入数据:包括初始形状数据和终止形状数据, 一般为事先定义好的整型变量数据,如简单的几何物体形状(苹果,凳子,陶罐)以及简单的动物形状(大象,马)等。也可以设计交互界面,用户通过界面交互输入数据。
插值算法:包括线性插值和矢量线性插值。
线性插值:对于初始和终止形状上每个点的坐标 $P_i$ 进行线性插值得到物体变形的中间形状;
矢量线性插值:对初始形状和终止形状上每两个相邻点计算其对应的矢量的长度和角度,然后对其进行线性插值得到中间长度和角度, 对起点帧和终点帧的第一个关键点进行线性插值得到中间图像的第一个关键点。顺序连接插值后定义的各个矢量得到中间变化形状。插值变量变化范围是[0,1], 插值变量等于 0 时对应于初始形状,插值变量等于 0 时对应于终止形状;数据类型为 double。
插值结果输出。用户可以在图形化界面中自行指定插值帧的个数以及动画刷新频率,程序会根据其设定的参数生成不同效果的关键帧动画并播放动画。用户可以通过点击不同插值方式的按钮,反复播放不同算法生成的插值结果。
三、 实验平台 Qt 5.14.2 @ Windows
四、 实验步骤 1. 线性插值: 指定两幅关键画面图形(最简单的是大小不同的两个矩形,分别由4个点构成。学生也可以自己构造更复杂的图形,如由若干点构成的手图形), 然后计算两幅图对应点的线性距离来得到它们的中间画面图形。
$$$ x_{ti} = x_0t + x_1 (1-t); t=1,…M; y_{ti} = y_0t + y_1 (1-t); $$$
线性插值代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 if (mode == 0) { inter_points.clear(); double t = 1.0 * time / grain; for (int i = 0; i < start_points.size(); i++) { QPoint temp; double x0 = start_points[i].x(); double y0 = start_points[i].y(); double x1 = end_points[i].x(); double y1 = end_points[i].y(); double x = (1 - t) * x0 + t * x1; double y = (1 - t) * y0 + t * y1; temp.setX(x); temp.setY(y); inter_points.push_back(temp); } }
2. 矢量线性插值: 与线性差值框架类似,但插值变量不再是线性插值中的点坐标表(x, y), 而是把图形曲线上每两个邻近点看成一个矢量,这样就能把由N 个点构成的曲线分解成 N-1 个矢量。初始图形的矢量记为$(a_{0i}, p_{0i})$,终止图形记为$(a_{1i},p_{1i})$,生成的中间图形记为$(a_{ti},p_{ti})$, 设生成 M 个画面,则有:
$$$ a_{ti} = a_0t + a_1 (1-t); t=1,…M; p_{ti} = p_0t + p_1 (1-t); $$$
矢量线性插值代码实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 //mode==1:普通矢量线性插值(不规定矢量插值方向) else if(mode==1) { inter_points.clear(); double t=1.0*time/grain; QPoint temp; double x0=start_points[0].x(); double y0=start_points[0].y(); double x1=end_points[0].x(); double y1=end_points[0].y(); double x=(1-t)*x0+t*x1; double y=(1-t)*y0+t*y1; temp.setX(x); temp.setY(y); inter_points.push_back(temp); for(int i=0;i<start_vectors.size();i++) { double vec_a0=start_vectors[i].a; double vec_p0=start_vectors[i].p; double vec_a1=end_vectors[i].a; double vec_p1=end_vectors[i].p; if(vec_a0<0)vec_a0+=2*PI; if(vec_a1<0)vec_a1+=2*PI; if(vec_a1-vec_a0>PI)vec_a0+=2*PI; if(vec_a1-vec_a0<-PI)vec_a1+=2*PI; double vec_a=(1-t)*vec_a0+t*vec_a1; double vec_p=(1-t)*vec_p0+t*vec_p1; x+=vec_p*cos(vec_a); y+=vec_p*sin(vec_a); temp.setX(x); temp.setY(y); inter_points.push_back(temp); } }
本次试验中,我还对矢量线性插值进行了三种不同的改良:分别是规定矢量顺时针旋转、规定矢量逆时针旋转以及规定矢量旋转角度小于π。
3. 编写paintWindow 类作为画板,继承自 QWidget 类。在 paintWindow 类中编写鼠标回调函数 mousePressEvent,记录通过鼠标交互选定的关键点。以及绘制函数paintEvent,在每次 update()时调用。paintWindow 类定义具体如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 class paintWindow : public QWidget { Q_OBJECT private: int grain; //每个曲线区间有多少个插值点(包括两端关键点) int speed; //刷新速度(改为int) int mode=0; //插值模式 int pen_index=0;//使用第几种笔刷 int time;//时间 QTimer* timer; //计时器 vector<QPoint> start_points;//储存起点帧点坐标 vector<Vector> start_vectors;//储存起点帧向量 vector<QPoint> end_points;//储存终点帧点坐标 vector<Vector> end_vectors;//储存终点帧向量 vector<QPoint> inter_points;//储存当前插值帧关键点 bool start_draw=false; //是否绘制起始帧图像 bool end_draw=false; //是否绘制终止帧图像 bool startframe=true; //是否处于起始帧选定状态 bool endframe=true; //是否处于终止帧选定状态 public: paintWindow(); void change_frame(); //从起始帧切换到终止帧 void finish_frame(); //结束终止帧交互 void calc_vectors(); //计算关键帧向量 void set_interpolation(int _grain,int _speed, int _mode); //设置动画参数 void paintEvent(QPaintEvent *); //绘制函数 void mousePressEvent(QMouseEvent *e); //鼠标回调函数 int numbers(); //关键点个数 void change_pen(); //改变笔刷 void clear(); //清屏 private slots: void changeState(); //连接计时器,改变小车坐标,旋转角度等信息 };
4. 鼠标回调函数 mousePressEvent,记录通过鼠标交互选定的关键点,储存在名为start_points 和 end_points 的vector 中。
1 2 3 4 5 6 7 //鼠标回调函数,鼠标点击,加入关键点 void paintWindow::mousePressEvent(QMouseEvent * e) { if (startframe)start_points.push_back(e->pos()); else if (endframe) end_points.push_back(e->pos()); update(); }
5. 绘制函数 paintEvent,根据数据变化,绘制所有的关键点,起始帧图像,以及中间插值图像。(篇幅限制,此处省略部分代码)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 //绘制函数 void paintWindow::paintEvent(QPaintEvent*) { QPainter paint(this); if (start_points.size() <= 0)return; //没有关键点6. //设置笔刷样式,绘制关键点 paint.setPen(QPen(Qt::black, 5, Qt::DashDotLine, Qt::RoundCap)); for (int i = 0; i < start_points.size(); i++) paint.drawEllipse(start_points[i], 1, 1); for (int i = 0; i < end_points.size(); i++) paint.drawEllipse(end_points[i], 1, 1); //设置笔刷样式,绘制起点帧图像 //paint.setPen(QPen(Qt::blue,3,Qt::SolidLine,Qt::RoundCap)); if (start_points.size() > 0) { if (start_draw) { for (unsigned int i = 0; i < start_points.size() - 1; i++) { QPoint p1 = start_points[i]; QPoint p2 = start_points[i + 1]; paint.drawLine(p1, p2); } QPoint p1 = start_points[0]; QPoint p2 = start_points[start_points.size() - 1]; paint.drawLine(p1, p2); } } //设置笔刷样式,绘制终点帧图像(省略) //设置笔刷样式,绘制插值帧图像 //paint.setPen(QPen(Qt::red,3,Qt::DotLine,Qt::RoundCap)); if (time != 0) { if (inter_points.size() > 0) { for (unsigned int i = 0; i < inter_points.size() - 1; i++) { QPoint p1 = inter_points[i]; QPoint p2 = inter_points[i + 1]; paint.drawLine(p1, p2); } QPoint p1 = inter_points[0]; QPoint p2 = inter_points[inter_points.size() - 1]; paint.drawLine(p1, p2); } } }
6. 引入QTimer 类作为计时器,每隔一段时间调用 changestate 函数, 在该函数中,改变当前插值图像信息。通过线性插值或者矢量线性插值计算,将当前插值图像的所有关键点坐标储存在名为inter_points 的vector 中。
7. MainWindow 设计及按钮槽函数 MainWindow 窗口设计如下:
五、 实验结果分析 分析不同起始帧和终止帧对应不同插值方法的效果和局限性:
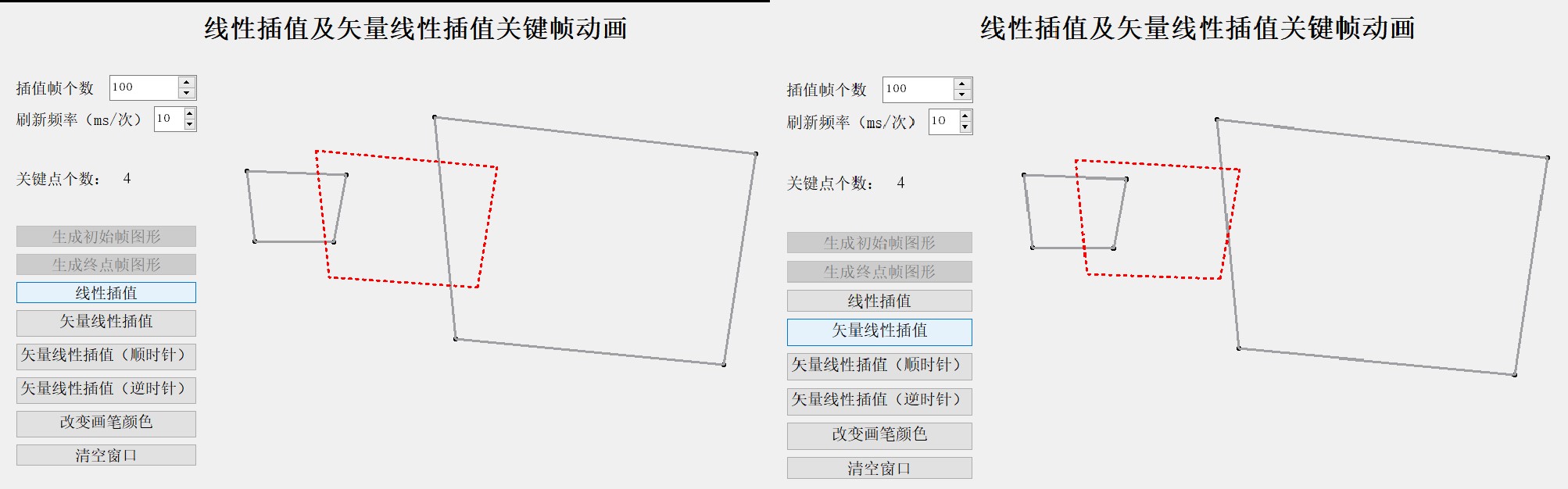
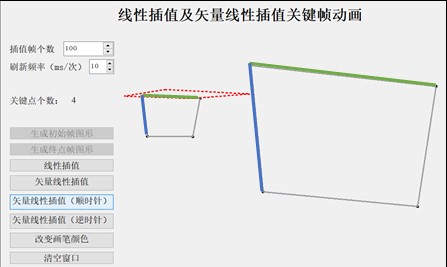
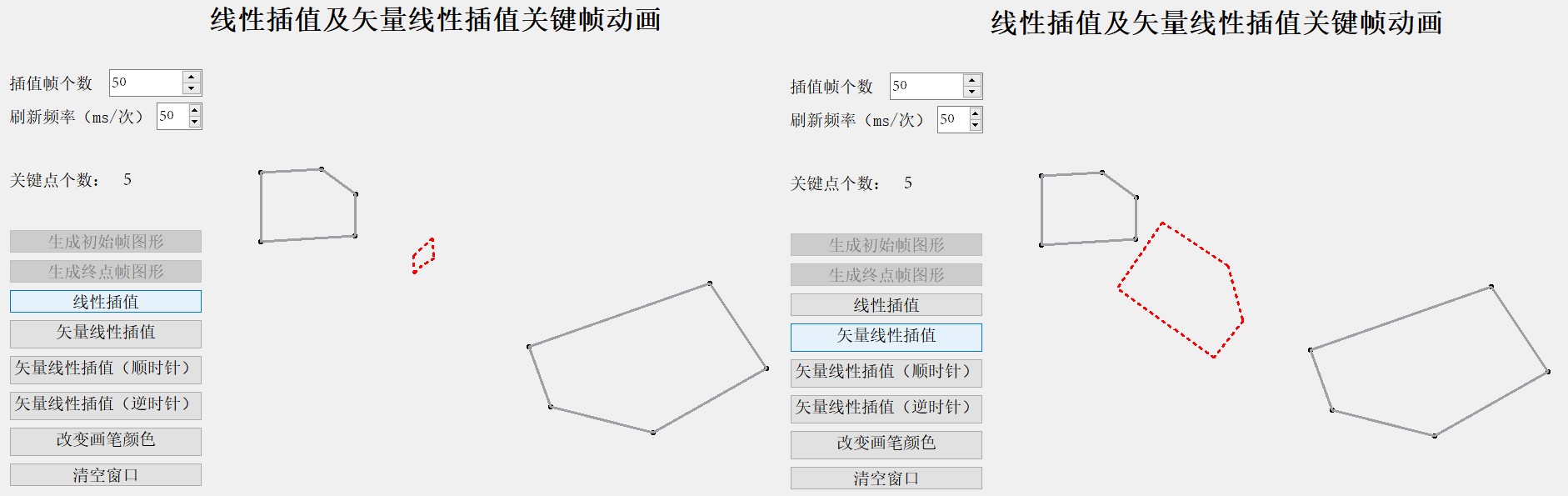
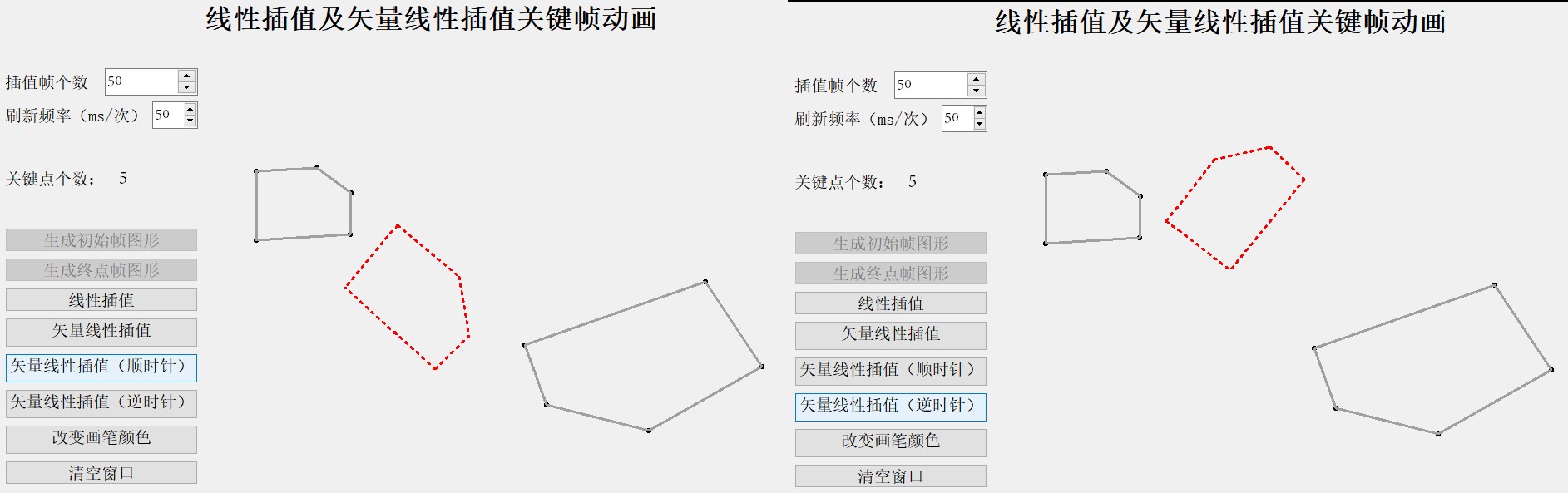
1) 普通四边形(几乎不旋转)
上图中绿色标注的边终点帧比起点帧的向量角度更小,而蓝色标注的边,则是终点帧比起点帧的向量角度更大,因此在选择向量顺时针插值时,绿色标注的边可以直接选择角度小于π的旋转方式,而蓝色标注的边则会选择大于π的旋转方式(几乎接近旋转一周),因此导致图像插值过程中变形。
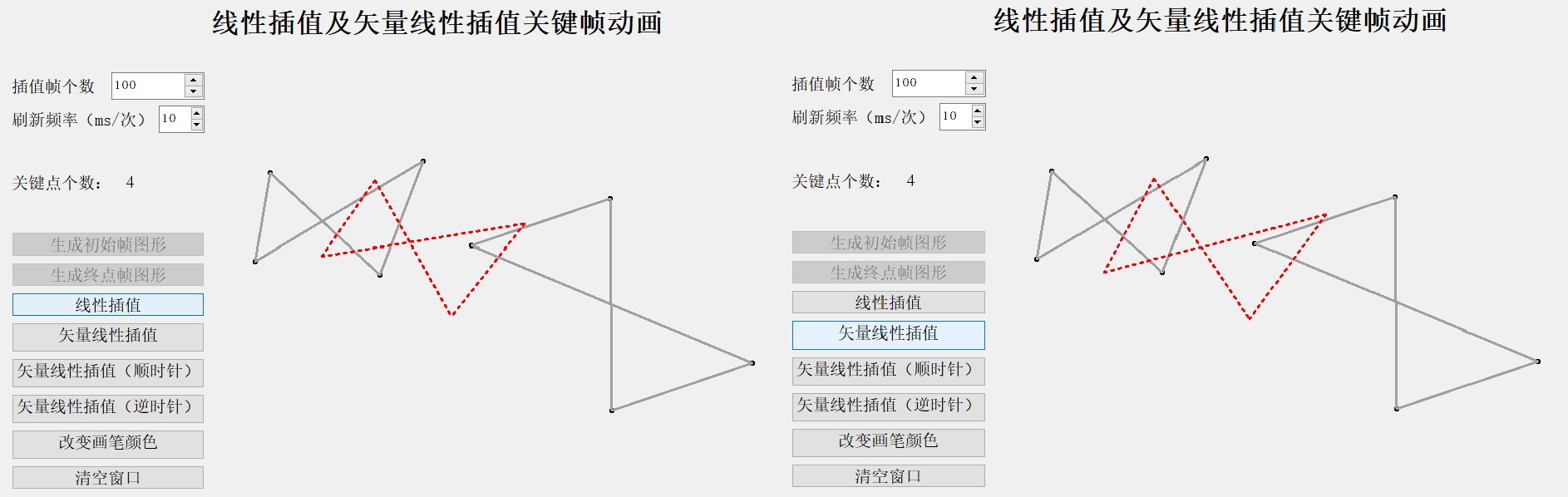
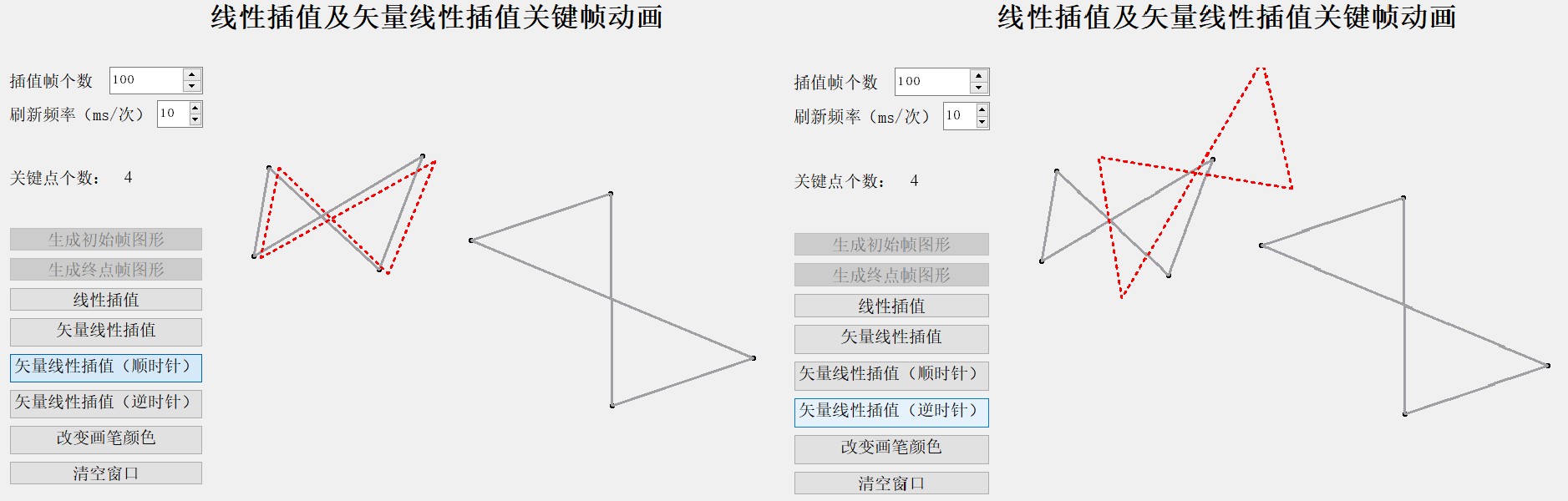
2) 边交叉的四边形(有一定的旋转角度(0 ~π/2))
可以看出上图中四种插值方式的效果都非常好,顺时针向量插值时,图像呈现顺时针转动效果,逆时针插值时效果相反。
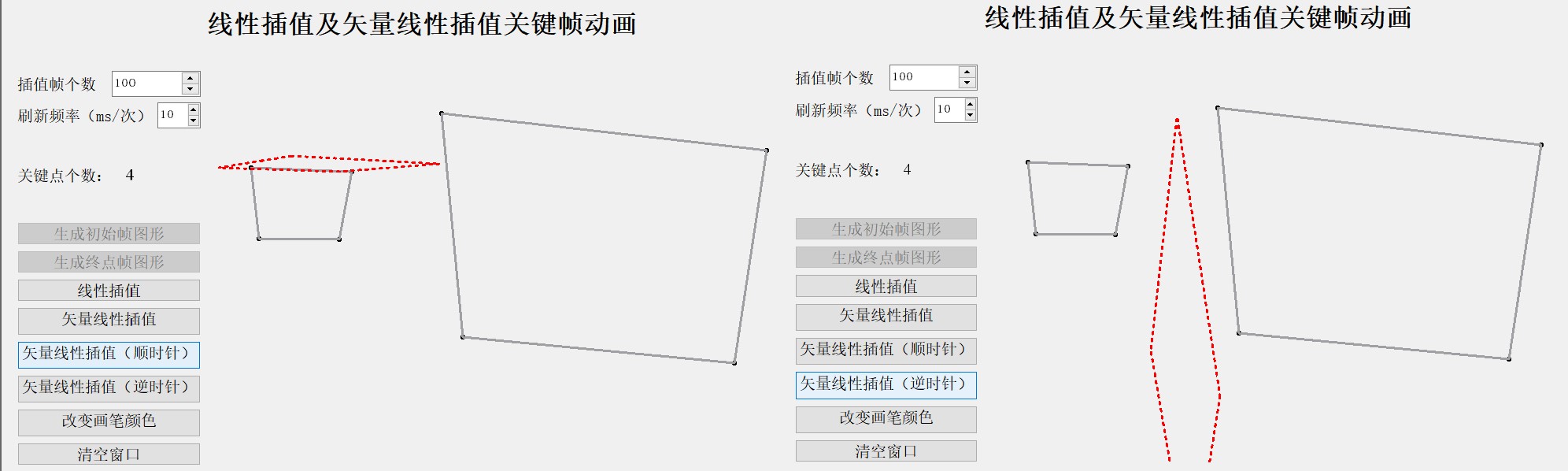
3) 小车大小变化(有一定的旋转角度(π/2 ~π))
可以看出上图中直接线性插值方式会产生明显的变形,不能保持形状平滑变化,而其他三种矢量线性插值方式效果都表现得非常好。
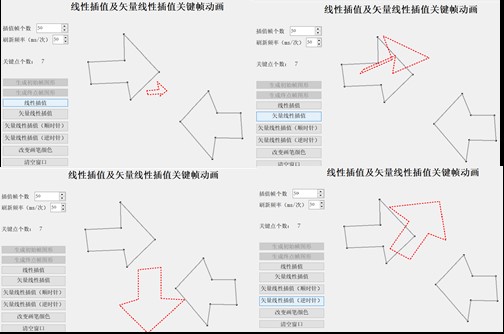
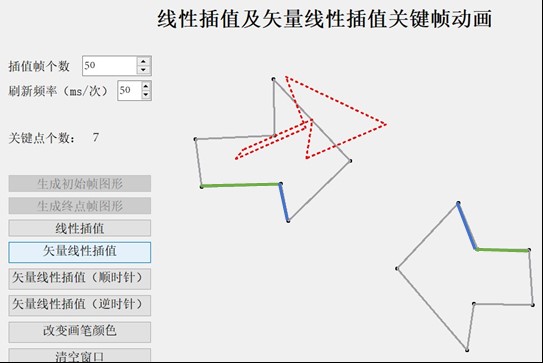
4) 箭头图形(旋转角度接近π)
可以看出上图中直接线性插值方式会产生明显的变形,不能保持形状平滑变化,第一种矢量线性插值方式也会产生非常严重的变形, 而规定了顺时针或者逆时针差值的矢量线性插值方式效果表现得非常好。
上图中绿色标注的边终点帧比起点帧的向量大一个接近π的值, 于是算法在判断后,认为该边应该逆时针旋转插值,而蓝色标注的边, 则是终点帧比起点帧的向量大一个稍大于π的值(也可以看成是小一个接近π的值),因此算法在判断后,认为该边应该顺时针旋转。这就导致了相邻的两个向量向着不同的方向旋转,因此导致图像插值过程中变形。
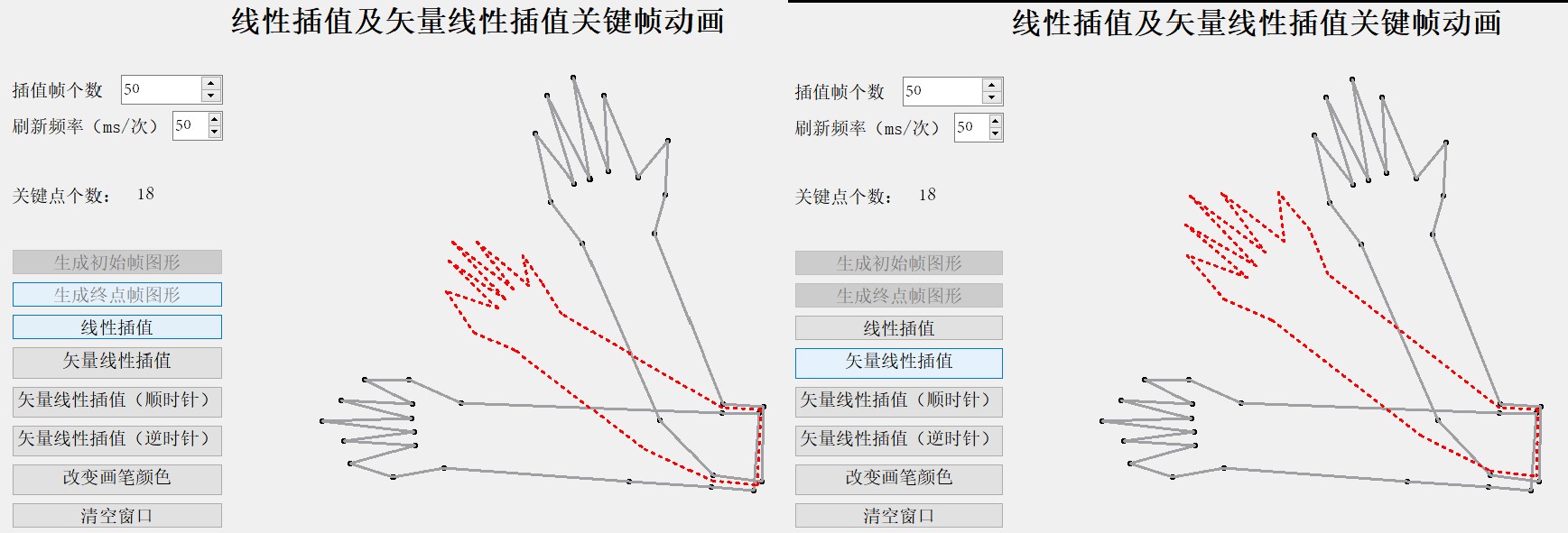
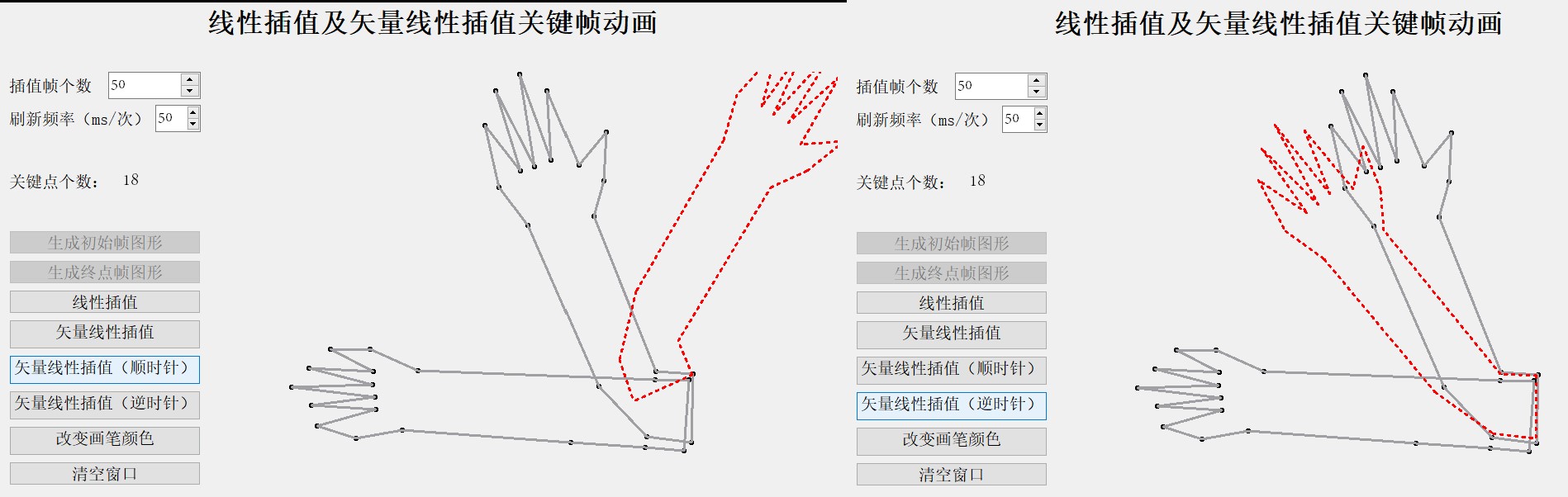
5) 复杂图像的关键帧插值动画
如上图,可以看出,除了线性插值有明显的变形之外,其他三种矢量差值方式都表现得效果非常好。
6) 分析总结 没有一种关键帧动画算法可以适用于所有的场景,通过对不同起始帧终止帧图像的情形的实践和分析,我总结出:
对于方向基本没有变化的初始帧和终止帧,普通线性插值效果非常不错,第一种矢量线性插值算法(规定矢量旋转角度小于π)也表现非常好,第二三种矢量线性插值算法(规定矢量旋转方向为顺时针或者逆时针)则可能会产生较大的变形,原因是相邻两个矢量旋转角度一个大于零一个小于零。
对于方向有一定变化(0~π)的初始帧和终止帧,普通线性插值算法会使得插值图像有较大的变形(一般情况下,旋转角度大的, 变形程度也会更大),而三种矢量线性插值算法都表现得效果非常好。
对于方向变化接近π的初始帧和终止帧,普通线性插值算法也会使得插值图像有较大的变形(一般情况下,旋转角度大的,变形程度也会更大),第二三种矢量线性插值算法(规定矢量旋转方向为顺时针或者逆时针)也表现非常好,第一种矢量线性插值算法(规定矢量旋转角度小于π)则可能会产生较大的变形,原因是相邻两个矢量旋转角度一个大于π一个小于零π。
对于方向变化较大(π~2π)的初始帧和终止帧,效果可以参考第二条。
以上所有总结建立在本实验程序的演示基础上,本实验中产生这些现象的主要原因是,不能保证初始帧和终止帧有完全相同的角度,如果在更多元化的图形化交互界面中,可以将初始帧直接复制放大缩小平移旋转得到终止帧,则每一种矢量线性插值算法都不会产生上述的严重变形现象。
但是在真正的动画制作中,也不可能保证初始帧和终止帧有完全相同的角度,因此本次实验的分析还是非常具有实际意义的。