计算机视觉HW2 - 直线检测和圆检测

课程名称：计算机视觉
实验项目名称：直线检测和圆检测

一、实验目的和要求

对输入的一张彩色图像，检测其中的圆形与直线，并将检测结果显示在原图上。

检测算法的核心功能需要自己写代码实现，不能调用 OpenCV 或其他SDK里与圆形直线检测相关的函数；如果要用到边缘检测，这个可以调用 OpenCV 函数。
在原图上显示最终的检测结果。
单独显示一些关键的中间结果
必须对指定的三张测试图像（ coin 、seal 、highway ）调试结果。此外，自己还可以自愿加一些测试图像。

二、实验原理

1）Hough 变换

图片alt
$$$
y=mx+c 　　\Rightarrow　　c=-xm+y
$$$
如上图，对于笛卡尔坐标系内的一条直线：$y=mx+c$

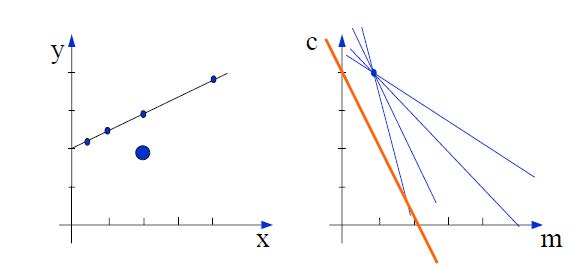
以$(x_0,y_0)$点为例，固定$x_0,y_0$为自变量，$(m,c)$为变量，则每个点$(x_0,y_0)$对应于空间$(m,c)$上的一条直线：$c=-xm+y$

通过变换坐标系，将直线和点相互转换，从而将求直线转化为求多条直线的交点。

但是上述转换存在直线垂直时，斜率是无穷大的情况，因此我们换用极坐标系。

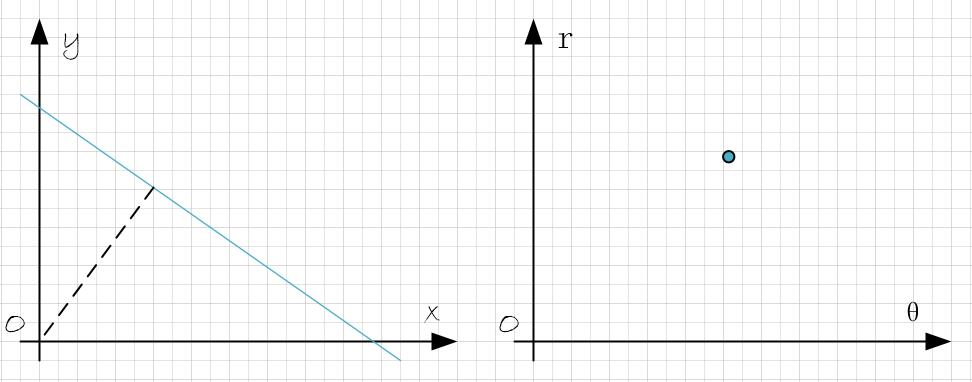
直角坐标系中的点是极坐标系中的线，直角坐标系中的线是极坐标系中的点。

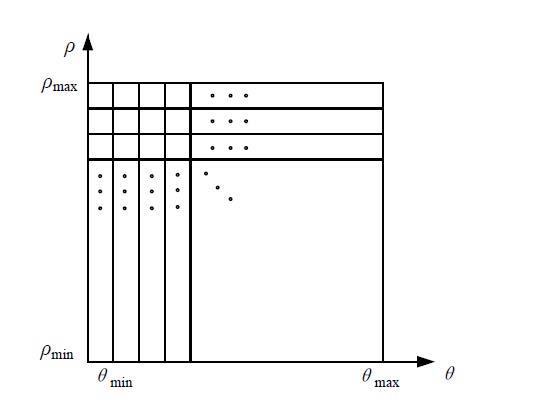
如下图所示，想要检测图像中的直线，可以使用Hough变换，转化为检测极坐标系中的点 $(\theta, \rho)$ 。

图片alt

2）直线Hough变换

笛卡尔坐标系中的直线，由斜率和截距表示，而极坐标中用 $(\theta, \rho)$ 表示，并且存在下式关系：
$$$
\rho = cos(\theta)\cdot x + sin(\theta)\cdot y
$$$
对于点 $(x_0,y_0)$，代入上式，在极坐标中就是一条线（很多对 $(\theta, \rho)$ 点）：
$$$
r = cos(\theta)\cdot x_0 + sin(\theta)\cdot y_0
$$$
$(\theta, \rho)$ 就是一对Hough空间的变量表示。一个点 $(x_0,y_0)$, 就是一个正弦曲线。

图片alt

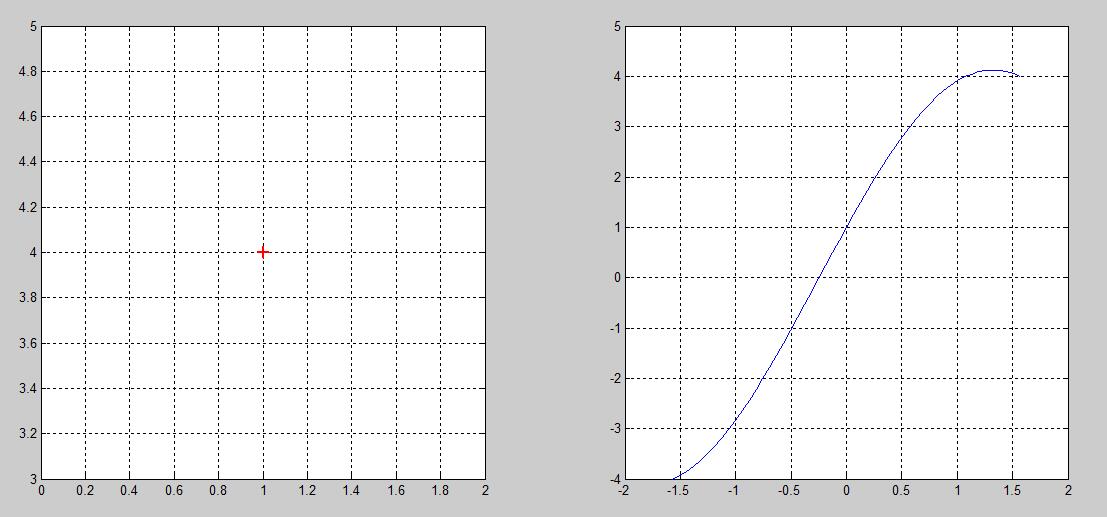
如下图，直角坐标系中的多个点，对应于 $\rho - \theta$ 空间的多条正弦曲线。

图片alt

直角坐标系的三点共线，对应于 $\rho - \theta$ 空间的多线共点。

因此，我们可以通过检测 $\rho - \theta$ 空间的交集点，来检测原始空间的线段。

接下来，就是要考虑将 $\rho - \theta$ 离散化，形成离散化的Hough空间，用于统计交集点的个数。

3）累加器

图片alt

将参数空间离散化，从而得到一个二维数组累加器，记录 $\rho - \theta$ 空间每对参数 $(\theta, \rho)$ 出现的次数，大于某个阈值的，就证明有线相交于该点，也就证明原笛卡尔坐标系中有直线。

4）圆的Hough变换

给定一个圆弧有三个参数，$a,b$用来确定圆心位置，$\rho$确定半径。
$$$
b=atan\theta-xtan\theta+y
$$$

类似直线，将$(x_0,y_0)$固定，而将$(a,b,\rho)$作为变量：
$$$
x=a+\rho cos \theta 　　 \Rightarrow　　 a=x-\rho cos \theta \
y=b+\rho sin \theta 　　　　　　 b=y-\rho sin \theta
$$$
因此可以创建hough三维累加器，对于圆图像中的每一个点计算对应的$(a,b,\rho)$点对。

但由于是三维累加器，会大大增加计算量。因此我们采用霍夫梯度法，先找出圆心的坐标。

我们令$\rho$为边缘点处的梯度角，则上面的公式可以变换为：
$$$
b = a tan\theta-x tan\theta+y
$$$
如下图，圆的边缘点切线的垂直方向,也就是梯度方向经过圆点。所以我们可以建立关于$(a,b)$的二位累加器，遍历图像的所有点，对每个像素点计算梯度（本实验中使用Sobel算子），对该直线上的所有像素点进行投票，最后选取超过阈值的像素点作为阈值，为了避免选取过多的圆心，把距离小于某一个阈值的圆心当做同一个圆心。

图片alt

下一步，对于每一个投票选出的圆心，遍历整个图像，计算他们与该圆心的距离，然后将距离值排序，在某一个距离范围区间内，点超过一定数量的，就可以将该距离作为该圆心对应的一个半径。

全部遍历完成后，就可以得到$(a,b,\theta)$点对表示的圆检测结果。

三、实验内容和过程分析

1) 主函数及图像读入和预处理流程分析

本实验中，读入图像后我对图像做了一下预处理：

转化为灰度图
高斯滤波以及均值滤波，图像去噪，防止噪声干扰边缘检测
使用Canny算子计算图像边缘并展示
将边缘图像作为掩码拷贝源图像，从而展示彩色的边缘图像

预处理之后进入正式的直线和圆形检测，调用“HoughLine”以及“HoughCircle”模块中的函数

使用Hough变换检测直线并返回结果，在源图像上绘制结果直线
使用Hough梯度法检测原型并返回结果，在源图像上绘制结果圆

以下是简化版的主函数代码，其中包括图像预处理以及直线和圆检测函数的调用（篇幅限制，仅展示主要内容）：

vector<Vec3f> circles;
vector<Line> lines;

//读入图像
Mat src = imread("1.jpg", 1);
if (!src.data)
{
	cout << "图像不存在！" << endl;
	return -1;
}
imshow("source", src);  	//展示源图像
waitKey(0);

Mat src_edge;	
cvtColor(src, src_gray, CV_BGR2GRAY);  //转换为灰度图

//高斯滤波，减弱噪声，避免检测时产生干扰
GaussianBlur(src_gray, src_gray, Size(9, 9), 2, 2);
imshow("guass", src_gray);
waitKey(0);
//对灰度图再做一次均值滤波
blur(src_gray, src_edge, Size(3, 3));
imshow("mean", src_edge);
waitKey(0);

//使用Canny算子计算图像边缘并展示
Mat edges;
int canny_threshold = 40;
Canny(src_edge, edges, MAX(canny_threshold / 2, 1), canny_threshold, 3);
imshow("edges", edges);
waitKey(0);

//使用Canny算子输出的边缘图，edges作为掩码，
//来将原图image拷贝到目标图dst中，从而显示彩色的边缘图像
Mat image = src.clone();
Mat dst;
dst.create(image.size(), image.type());
dst = Scalar::all(0);
image.copyTo(dst, edges);
imshow("colorful_edge", dst);
waitKey(0);

//hough检测圆形并返回结果
houghcircles(src_gray, edges, circles, 10, 40, 30, 0, 0);
//在原图像上绘制检测到的圆形并输出结果
for (size_t i = 0; i < circles.size(); i++){
	Point center(cvRound(circles[i][0]), cvRound(circles[i][1]));
	int radius = cvRound(circles[i][2]);
	circle(src, center, 3, Scalar(0, 255, 0), -1, 8, 0);  //圆心
	circle(src, center, radius, Scalar(255, 0, 0), 2, 8, 0);  //圆
}
//hough检测直线并返回结果
houghlines(edges, lines, 110);
//在原图像上绘制检测到的直线并输出结果
for (size_t i = 0; i < lines.size(); i++){
	Point s = lines[i].start;
	Point e = lines[i].end;
	line(src, s, e, Scalar(0, 0, 255));
}
//展示绘制结果后的图像
namedWindow("Result", CV_WINDOW_AUTOSIZE);
imshow("Result", src);
waitKey(0);

2）Hough变换检测直线

HoughLine模块结构体及函数原型

// ρ-θ空间累加器
struct Polar{
    int x;
    int y;
    int count;
};
//用于返回直线两端的坐标
struct Line{
    Point start;
    Point end;
};
bool polar_order(Polar a, Polar b);  //用于排序
int get_position(Mat img, int ii, int jj, int flag);  //对于水平和垂直的直线，找回Hough变换时损失的信息
//hough变换检测直线
//img：输入的边缘图像（灰度图，只有0,255两个值）
//lines：储存最后检测出的直线起始点
//threshold：累加器阈值，只有累加器中的值大于该值，该参数对才会被选中
//rho：ρ参数的分辨率（遍历步长）
//theta：θ参数的分辨率（遍历步长）
void houghlines(Mat img,vector<Line>& lines, int threshold, double rho = 1, double theta = 1);

适当地量化参数空间（合适的精度即可）

根据图像大小及分辨率（精度）计算累加器大小

//图像长宽
int w = img.cols;
int h = img.rows;
//累加器大小
int add_w = 180/theta;
int add_h = 1.5 * (w + h) /rho ;
//消除值为负的ρ
int center_h = add_h / 2;

假定参数空间的每一个单元都是一个累加器，把累加器初始化为零

//为累加器分配空间
   int** add = (int**)malloc(add_h * sizeof(int*));
   for (int i = 0; i < add_h; i++)
       add[i] = (int*)malloc((add_w + 1) * sizeof(int));

   //累加器赋值为0
   for (int i = 0; i < add_h; i++)
       for (int j = 0; j < add_w; j++)
           add[i][j] = 0;

对图像空间的每一点，在其所满足的参数方程对应的累加器上加1

//累加器投票
   int threshold_pix = 200;
   for (int i = 0; i < h; i++)
       for (int j = 0; j < w; j++)
           if ((int)img.at<uchar>(i, j) > threshold_pix)
               for (int k = 0; k < 180; k=k+theta) {
                   double angle = (double)k / 180 * PI;  //角度制转换为弧度值
                   double dr = (double)j * cos(angle) + (double)i * sin(angle);
                   int r = round(dr)/rho;
                   int kk = k/theta;
                   add[r + center_h][kk]++;  //r可为负值，加上矩阵中心                  
               }

累加器阵列的超过阈值的点对应直线的参数

在这里对原算法进行了改进，判断累加器是，需要该点同时满足值超过阈值和大于自身周围的点的累加器值，才将该点选中。

并且在选中点之后，对其做一个聚合操作，即将其周围一定区间内的累加器的值也看做是一条直线，同时累加给该点。

（原理相似处代码此处省略）

//遍历累加器，选出符合规定的ρ-θ点对作为检测到的直线参数
vector<Polar> v;  
for (int y = 1; y < add_h - 1; y++)//模长
{
    for (int x = 0; x < add_w; x++)//角度
    {
        int flag = 0;
        //如果当前点在累加器边界处
        if (x == 0)
            if (add[y][x] > threshold && add[y][x] > add[y][x + 1] && 
                add[y][x] > add[y - 1][x] && add[y][x] > add[y + 1][x]) flag = 1;
        else if (x == add_w - 1) //此处省略
        //如果当前的值大于阈值，并在4邻域内它是最大值，则该点被认为是圆心
        else if (add[y][x] > threshold && add[y][x] > add[y][x - 1] &&
            add[y][x] > add[y][x + 1] && add[y][x] > add[y - 1][x] &&
            add[y][x] > add[y + 1][x])  flag = 1;
        //选择该点表示的参数作为一条直线的参数
        if (flag)
        {
            Polar po;
            po.x = y;    //ρ
            po.y = x;    //θ
            po.count = add[y][x];
            //聚合，如果当前参数对被选中，则把相邻(-5,5)区间内的累加器值都加给它
            for (int p = y - 5; p <= y + 5; p++)
                for (int q = x - 5; q <= x + 5; q++)
                    if (p >= 0 && p <= add_h - 1 && q >= 0 && q <= add_w - 1)
                        po.count += add[p][q];

            v.push_back(po); //当前点符合要求，作为圆心
        }
    }
}

将结果记录到lines

对已经被选中的点降序排列后，反推计算出其在原图像中对应的直线的起始点坐标，并记录到lines中。（此处代码简化）

在这里分四种情况处理：
- 水平直线
- 垂直直线
- $\theta$ 较小
- $\theta$ 较大

//对检测到的参数对按照累加器中的值大小降序排列
   sort(v.begin(), v.end(), polar_order);
   //将投票数最多的直线转换到笛卡尔坐标系计算出起始点坐标并存入名为lines的vector
   vector<Polar>::iterator iter;
   for (iter = v.begin(); iter != v.end(); iter++) {
       if (iter->y == 0)
       {
           y1 = 0;
           y2 = h - 1;
           x1 = x2 = get_position(img, iter->x, iter->y, false);
           Line temp;
           temp.start = Point(x1, y1);
           temp.end = Point(x2, y2);
           lines.push_back(temp);
       }
       else if (iter->y == 90){//此处省略}
       else if (iter->y >= 45 && iter->y <= 135) {//在这个范围内sin值比较大，使用sin做分母误差较小
           x1 = 0;
           y1 = (iter->x - center_h) / si; //加上之前为了消除ρ的负值减去的值
           x2 = w - 1;
           y2 = ((iter->x - center_h) - (double)x2 * co) / si;
           Line temp;
           temp.start = Point(x1, y1);
           temp.end = Point(x2, y2);
           lines.push_back(temp);
       }
       else { //在这个范围内cos值比较大，使用cos做分母误差较小     //此处省略 
       }
   }

3）Hough梯度法检测圆形

HoughCircle模块结构体及函数原型

#define PI  3.14159265358979
#define HOUGH_CIRCLE_RADIUS_MIN						10  //圆最小半径
#define HOUGH_CIRCLE_RADIUS_MIN_DIST				2   //同心圆两个半径最小差
#define HOUGH_CIRCLE_INTEGRITY_DEGREE				0.6  //用于判断圆周上的点是否足够多（是否能成圆）
#define HOUGH_CIRCLE_SAMEDIRECT_DEGREE				0.99  //用于梯度检测
#define HOUGH_CIRCLE_GRADIENT_INTEGRITY_DEGREE		0.9   //用于梯度检测

//记录圆心
struct Centers2
{
    int x;
    int y;
    int count;
};
bool center_order(Centers2 a, Centers2 b);  //用于排序

//记录其他点与圆心的距离和内积
struct Radius
{
    double dist2;
    double inner_product;
};
bool radius_order(Radius a, Radius b);  //用于排序
float normalization(float x);  //用于归一化圆心检测图像并放大差异，从而使圆心识别效果更好

//hough梯度法检测圆形
//src_gray：灰度图像
//edges：边缘图像
//circles：储存结果圆参数
//min_dist：两圆心之间的最小距离，小于该距离两圆心将被合并
//add_threshold：阈值，累加器中大于该值的点才能被选定为圆心
//min_Radius：圆最小半径
//min_Radius：圆最大半径
void houghcircles(cv::Mat& src_gray, Mat edges, std::vector<cv::Vec3f>& circles,
    double min_dist, int param2, int minRadius = 0, int maxRadius = 0);

量化关于a，b的参数空间到合适精度，创建并初始化累加器

//根据分辨率计算累加器的大小 dp为分辨率，此处为1
int add_rows = (double)src_gray.rows / dp + 0.5;
int add_cols = (double)src_gray.cols / dp + 0.5;

//创建累加器矩阵并为累加器分配内存
int** add = (int**)malloc(add_rows * sizeof(int*));
for (int i = 0; i < add_rows; i++)
	add[i] = (int*)malloc((add_cols) * sizeof(int));

//累加器赋值为0
for (int i = 0; i < add_rows; i++) 
	for (int j = 0; j < add_cols; j++) 
		add[i][j] = 0;

计算图像空间中边缘点的梯度幅度和角度，遍历边缘图像，若边缘点参数坐标满足则该参数坐标对应的累加器加1

使用Sobel算子计算边缘图像梯度，并根据分辨率遍历边缘图像计算累加器（篇幅限制，部分细节代码省略）。

//使用Sobel算子计算水平梯度和垂直梯度
cv::Sobel(src_gray, dx, CV_16SC1, 1, 0, 3);
cv::Sobel(src_gray, dy, CV_16SC1, 0, 1, 3);
Point pt;
//记录累加器中的最大值
	int accum_max = 0;
//遍历边缘图像
for (int y = 0; y < rows; y++)
{
	for (int x = 0; x < cols; x++)
	{
		//如果当前的像素不是边缘点，或者水平梯度值和垂直梯度值都为0
		if (!edges_row[x] || (dx_now == 0 && dy_now == 0))continue;
		//计算当前点的梯度模长
		float length = sqrt(dx_now * dx_now + dy_now * dy_now);
		//单位梯度向量所对应的水平和垂直的位移，作为遍历时的步长
		sx = cvRound((dx_now / dp) / length * ONE );
		sy = cvRound((dy_now / dp) / length * ONE );
		//当前点的坐标按照相同比例映射到累加器坐标
		int x_now = cvRound((x / dp) * ONE); 
		int y_now = cvRound((y / dp) * ONE);			
		//在梯度向量的正反两个方向分别计算累加器
		for (int times = 0; times < 2; times++)
		{
			//初始化坐标值，最小半径对应的位移
			x1 = x_now + minRadius * sx;
			y1 = y_now + minRadius * sy;
			//控制圆的半径在一定范围之内
			for (r = minRadius; r <= maxRadius; x1 += sx, y1 += sy, r++)
			{
				int x2 = x1 >> SHIFT, y2 = y1 >> SHIFT; //按照比例缩放回真实大小
				add[y2][x2]++;  //在累加器的相应位置上加1
				if (add[y2][x2] > accum_max) accum_max = add[y2][x2]; //记录累加器中最大的值
			}
			sx = -sx; sy = -sy; //把位移量设置为反方向
		}
		pt.x = x; pt.y = y;
		points.push_back(pt);  //记录边缘图像中的当前点
	}
}

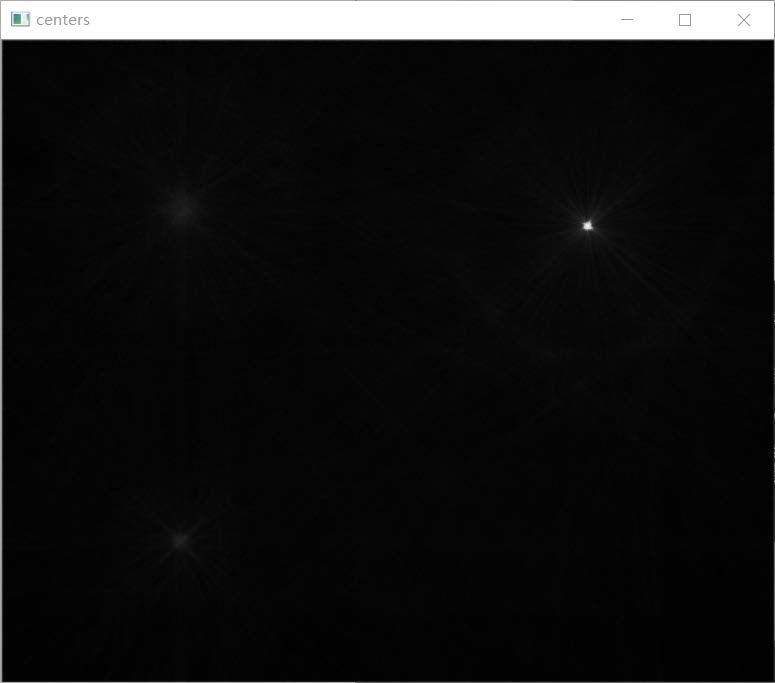
选出累加器的值大于一定阈值且局部最大的点，所在的坐标即为图像空间中的圆心之所在，并展示圆心选择结果

//对累加器做归一化和放大差异
for (int y = 1; y < add_rows - 1; y++)
	for (int x = 1; x < add_cols - 1; x++)
		add[y][x] = normalization((float)add[y][x] / accum_max) * 256;

//遍历累加器
for (int y = 1; y < add_rows - 1; y++)
	for (int x = 1; x < add_cols - 1; x++)
		//当前值是阈值且局部最大
		if (add[y][x] > add_threshold && add[y][x] > add[y][x - 1] &&
			add[y][x] > add[y][x + 1] && add[y][x] > add[y - 1][x] &&
			add[y][x] > add[y + 1][x])  {	
			Centers2 temp; //将当前点作为圆心
			temp.x = x;
			temp.y = y;
			temp.count = add[y][x];
			centers2.push_back(temp);
		}
//展示选择圆心的图像
Mat center_img = Mat(add_rows, add_cols, CV_32SC1);
for (int i = 0; i < rows; i++)
	int* ptmp = center_img.ptr<int>(i);
	for (int j = 0; j < cols; j++)
		center_img.at<int>(i, j) = add[i][j];
cv::normalize(center_img, center_img, 0, 255, cv::NORM_MINMAX);
center_img.convertTo(center_img, CV_8UC1);
imshow("centers", center_img);
waitKey(0);

得到圆心坐标之后，反求圆心对应的半径ρ

外层遍历得到的圆心，内层遍历所有参与计算的边缘图像中的点，计算他们与当前圆心的距离，并记录所有距离数据在名为Radius的vector中，对vector进行排序，之后遍历vector，对于在参数min_Radius范围内，圆周上的点数目大于一定阈值的半径，则作为该圆心对应的半径之一（考虑同心圆）。（代码部分省略）

//将圆心序列按照累加器中的数目降序排序
sort(centers2.begin(), centers2.end(), center_order);
//最小距离的平方
min_dist *= min_dist;

//按照累加器中的值由大到小的顺序遍历整个圆心序列
for (i = 0; i < centers2.size(); i++)
{
	radius.clear();
	int y = centers2[i].y;
	int x = centers2[i].x;
	//计算圆心在输入图像中的坐标位置
	float cx = (float)((x + 0.5f) * dp), cy = (float)((y + 0.5f) * dp);
	float start_dist, dist_sum;
	//判断当前的圆心是否之前已经输出过（如果距离小于min_dist，则判定为同一个圆心）
	for (j = 0; j < circles.size(); j++){
		cv::Vec3f center = circles[j];
		if ((center[0] - cx) * (center[0] - cx) + (center[1] - cy) * (center[1] - cy) < min_dist) 
               break;
	}
	if (j < circles.size())continue;

	//遍历之前记录的边缘图像中的所有点
	for (j = k = 0; j < points_count; j++){
		cv::Point pt;
		pt = points[j];
		//计算边缘图像中的点与当前圆心的距离
		float _dx = cx - pt.x;  float _dy = cy - pt.y;
		float _r2 = _dx * _dx + _dy * _dy;
		short sx = dxdy_row[0];
		short sy = dxdy_row[1];
		//记录所有在范围内的距离
		if (minRadius2 <= _r2 && _r2 <= maxRadius2){
			k++;
			Radius temp;
			temp.dist2 = _r2;
			radius.push_back(temp);
		}
	}
	//k表示一共有多少个圆周上的点
	int point_cnt1 = k, start_idx = point_cnt1 - 1;
	if (point_cnt1 == 0) continue;       
	//求平方根
	for (int t = 0; t < point_cnt1; ++t) 
		radius[t].dist2 = pow(radius[t].dist2, 0.5);
       
	//对圆半径进行排序，按累加器中的值降序排列
	sort(radius.begin(), radius.end(), radius_order);

	start_dist = radius[0].dist2;
	//遍历之间计算的半径，选择符合条件的半径
	for (j = 0; j <point_cnt1; j++)
	{
		float dist2 = radius[j].dist2;
		float inner_product = radius[j].inner_product;
	
		if (dist2 > maxRadius) break;
		if (dist2 - start_dist < HOUGH_CIRCLE_RADIUS_MIN_DIST * dr){    
			cur_r_count++; //记录圆周点个数
			cur_r_dist_sum += dist2;
		}
		//边缘图像上的圆周点足够多，判断圆是否合格
		else {
			float r_mean = cur_r_dist_sum / cur_r_count; //计算平均半径
			if (cur_r_count >= HOUGH_CIRCLE_INTEGRITY_DEGREE * 2 * PI * r_mean) {
				cv::Vec3f c;
				c[0] = cx;    //圆心的横坐标
				c[1] = cy;    //圆心的纵坐标
				c[2] = (float)r_mean;    //所对应的圆的半径
				circles.push_back(c);    //压入序列circles内				
			}
			cur_r_count = 1;
			cur_r_dist_sum = dist2;
			start_dist = dist2;			
		}
	}
}

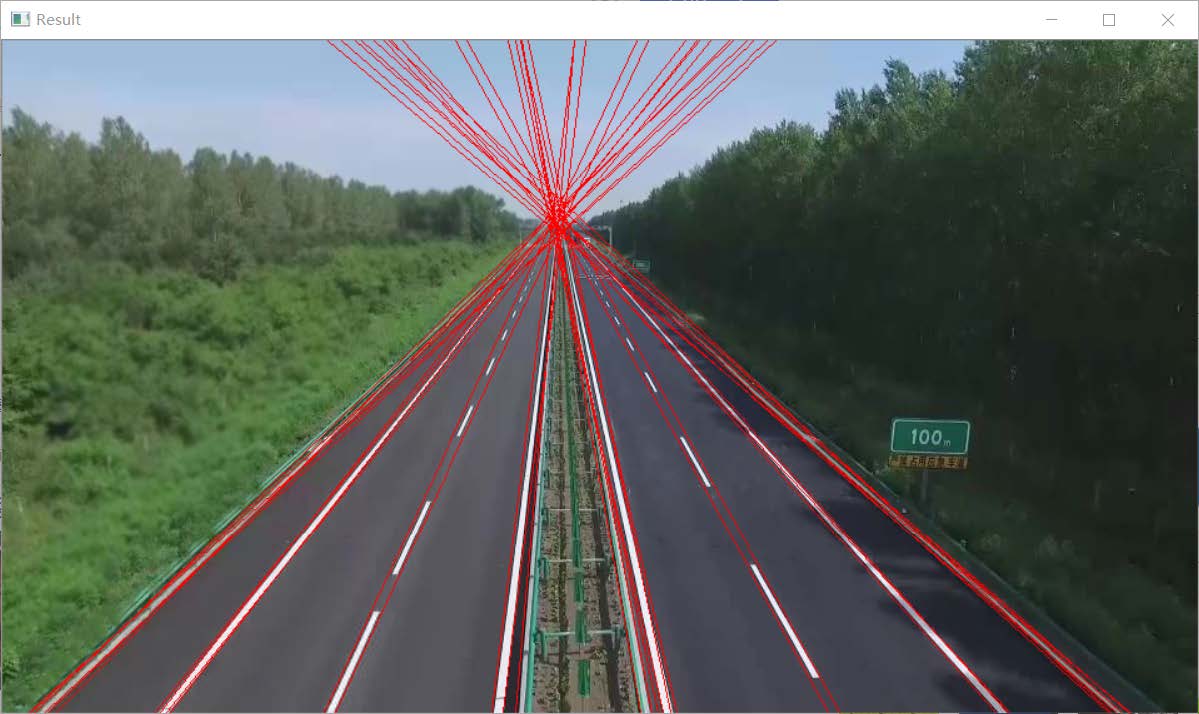
四、实验结果展示

1）直线检测（以highway图像为例）

该图像由于噪点较多，影响检测，因此实际实验时将高斯滤波和均值滤波的参数调大。

源图像

图片alt

滤波结果（此处仅展示高斯滤波结果，提交的压缩包中将含有高斯滤波和均值滤波）

图片alt

边缘图像（此处仅展示黑白边缘图像，提交的压缩包中将含有黑白和彩色两种格式）

图片alt

直线检测结果

图片alt

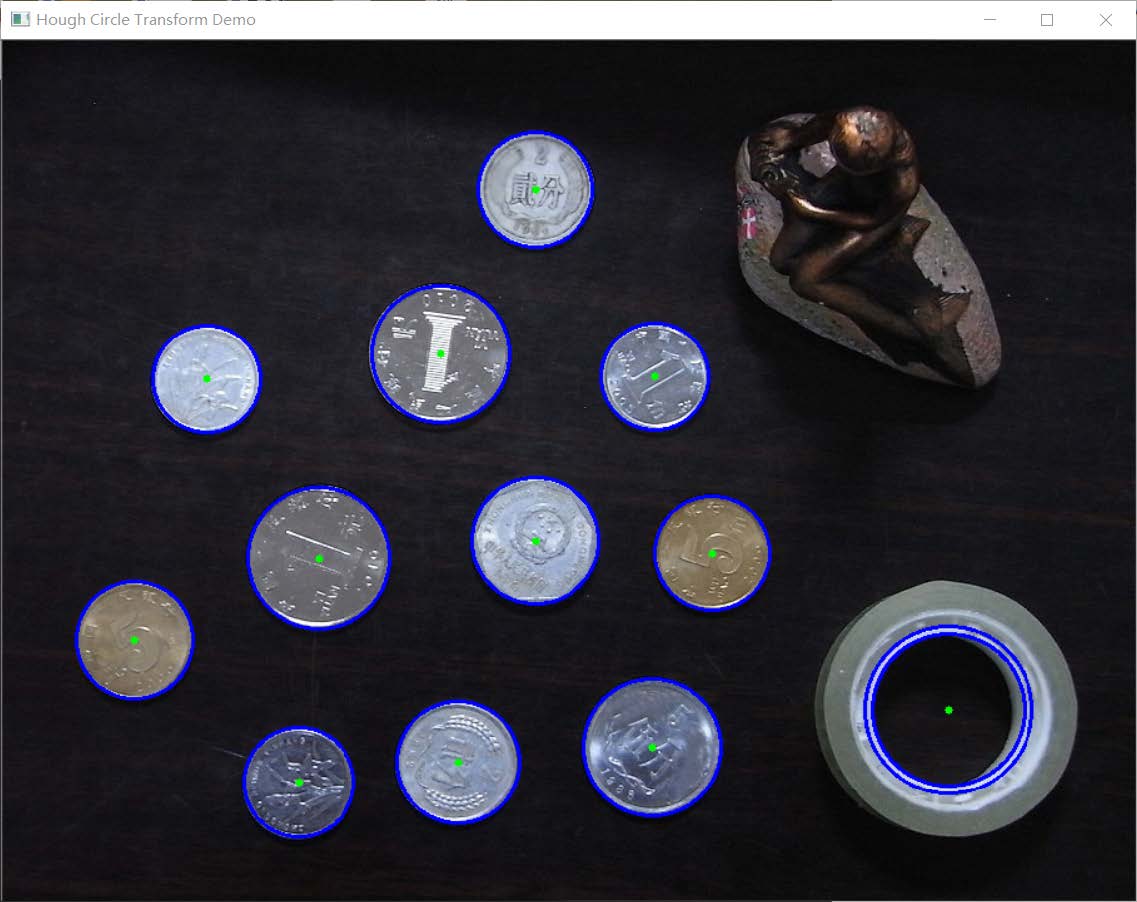
2）圆形检测（以coins图像为例）

源图像

图片alt

滤波结果（此处仅展示高斯滤波结果，提交的压缩包中将含有高斯滤波和均值滤波）

图片alt

边缘图像（此处仅展示黑白边缘图像，提交的压缩包中将含有黑白和彩色两种格式）

图片alt

圆心累加器结果

图片alt

圆形检测结果

图片alt

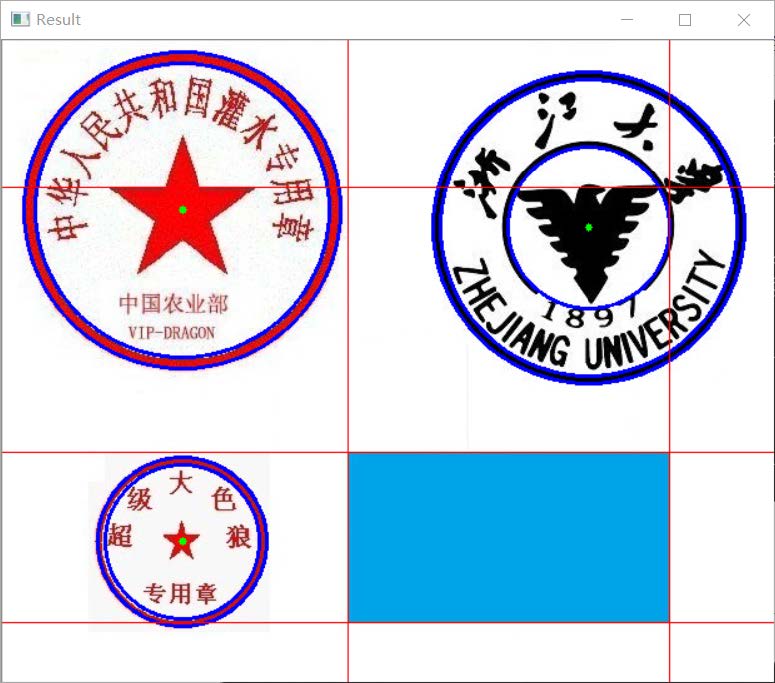
3）同时检测直线和圆（以seal图像为例）

1.源图像

图片alt

滤波结果（此处仅展示高斯滤波结果，提交的压缩包中将含有高斯滤波和均值滤波）

图片alt

边缘图像（此处仅展示黑白边缘图像，提交的压缩包中将含有黑白和彩色两种格式）

图片alt

圆心累加器结果
直线和圆形检测结果

五、实验思考和感想

通过本次实验，我更加深入地学习和体会了hough变换检测图形的算法，在实践的过程中，我发现了很多在学习过程中没有注意到的细节，都需要在实践进行调整。

在实验初期，调整hough变换检测的阈值是一件非常困难的事情，不合适的阈值对检测结果的影响非常大，后期，我发现这个阈值由于是一个绝对值，而图像大小会导致不同的图像适合的阈值有非常大的差别，因此我将其中的highway图像大小进行了调整，使其与其他两张图像大小差别缩小，因此最后的实验结果中，不必人为调整阈值，就可以同时对三张图像进行检测。

在实验中，我还发现，在进行直线检测时，由于hough变换时转换计算有误差，可能会导致变换后的线（对应原来的共线的点）不准确相交于一个点，而是在一个很小的范围内波动，因此我对算法进行了改进，在检测到累加器中的局部极大值后，在一个小范围区间内，对累加器的值做一个聚合，就会很大程度上避免这种情况，也能使得检验结果更加清晰准确。

另外，由于highway图像较模糊，清晰度较低，因此两旁的数目对检测结果的影响非常大，这是因为树木范围中很多点都被识别成了边缘点，因此，对于这张图像，我增大了均值滤波的参数，成功降低了树木中的边缘点数目，也最终非常明显地改善了检测结果。

在识别圆形时，我发现算法对于同心圆的检测效果不是那么优秀，我对算法进行了一定的改进，调整了宏定义的 “HOUGH_CIRCLE_RADIUS_MIN_DIST” 参数，使得计算半径时的半径区间范围稍微放大一些，从而使得半径的容错率更高，改善了半径计算不准确导致的无法识别出圆，将其舍弃的情况。但是该参数调整反馈非常敏感，稍微调整一点都会很明显地影响到检测结果（可能识别出一些不合适的结果，如下图），因此最后很遗憾地是还是没能识别出胶带最外圈的圆形，而只识别出了两圈（见上文图片）。但是经过对原图像和边缘图像的分析，我们也可以看出，出现这种结果的原因可能是因为：胶带内圈的两个圆太密集，从而使得算法可能检测出小圆的左半圈和右半圈为一个整圆，才会出现下图的结果。因此最后还是将该参数调回了原来的值。

图片alt