课程名称:基于GPU的渲染
项目主题名称:布料真实感实时渲染
日期:2022 年 1 月 10 日
PS: 当时还比较年轻,有些问题略弱智。
〇. Part Zero 基本概述及project组织架构
基本概述:
本次大程为了实现布料的实时渲染,我的主要思路是使用PBR的渲染方式,通过使用Albedo、Normal Map、Roughness Map等贴图,完成布料的基本着色。
阴影部分采用ShadowMap算法实现,使用PCF算法完成对阴影锯齿状走样的消除和处理,得到软阴影。
实验中用到的贴图均为本人使用Substance Painter绘制后烘焙导出。另外为了使工程文件格式统一,我还对模型进行了一些预处理。
在后文我将对本次大程中的几个重要部分的原理分别阐述。
Project组织架构:
实验环境及用到的库:
请使用 Release x86 生成解决方案和调试。
需要的头文件、lib文件已经打包在项目目录下,并在项目属性配置中用相对路径引用。
- 需要的dll文件放在项目目录下。
- main.cpp为主要源文件,主函数入口在其中,核心的渲染过程也在该源文件中。
- Fonts文件夹下是几个字体,字体用于显示Text(比如FPS显示)。
- include文件夹是需要的头文件,主要是Glad、GLFW等库的头文件
- lib文件夹是用到的库的lib文件
- Headers文件夹下是工程中一些模块的头文件,比如Camera模块、Shader模块等等。
- Models文件夹下是用到模型文件,编号表示模型内容、所属人物和姿势。比如”body1_1“表示第一个人物的第一个姿势,”cloth1_1“表示第一件衣服的第一个姿势,cloth1-cloth3属于第一个人物,cloth4-cloth6属于第二个人物。
- Shaders文件夹下是需要的shader源文件,其中PBRShader是本次项目主要使用的shader,RenderTexture是将ShadowMap展示在窗口使用的shader。
- Textures文件夹下是使用的贴图,background为前缀的贴图是背景幕布的贴图。set1文件夹下存放女孩模型使用的贴图,set2文件夹下存放男孩模型使用的贴图,其中,两个body的渲染使用的是一样的贴图。每套贴图共有5张,编号从0到4分别是Albedo、Normal Map、Metallic Map、Roughness Map、AO Map。其中由于没有使用到Metallic和AO贴图,因此有些地方直接将这两张贴图省略了。
Ⅰ. Part One PBR基本原理
PBR(Physically Based Rendering),指的是基于物理的渲染,更符合物理学规律,看上去更真实。并且由于其与真实的物理性质非常接近,可以直接用物理参数为依据来编写表面材质。由于基于物理的渲染旨在以一种物理上合理的方式模拟光,因此与我们的原始照明算法(如Phong和Blinn-Phong)相比,它通常看起来更真实,并且非常接近实际物理,我们可以根据物理参数编写表面材料,而不必求助于廉价的技巧和调整来使灯光看起来正确。基于物理参数编写材质的一个更大的优点是,无论照明条件如何,这些材质都会看起来正确。
满足基于物理渲染的三个条件:
- 基于微平面(Microfacet)的表面模型
- 能量守恒
- 应用基于物理的BRDF
微平面模型
- 达到微观尺度之后,任何平面都可以用被称为微平面的细小镜面来描绘。
- 微平面的取向排列的不一致程度,与平面粗糙程度有关。平面越粗糙,微平面排列越混乱。
- 对于粗糙平面,入射光线更趋向于向完全不同的方向发散,光滑平面上,入射光线大体上趋向于向同一个方向发射。
- PBR中一般基于光线向量l和视线向量v的中间向量h与微平面平均取向方向的一致性计算镜面反射。
- 中间向量计算公式:$h = \frac{l+v}{||l+v||}$
- 微平面无法逐像素区分,因此应该假设一个粗糙度参数,并使用统计学方法估算微平面的取向方向。
- 粗糙度系数取值为0-1之间,可以估算微平面的取向情况。
- 粗糙度越高,镜面反射轮廓越大,反之轮廓越小但边缘更锐利。
能量守恒
- 微平面近似法中的能量守恒:出射光线的能量永远不能超过入射光线的能量(发光面除外)。
- 一束光线碰撞到一个表面时,会分离成一个折射部分和一个反射部分。反射部分不进入平面直接反射,成为镜面光照。折射部分会进入表面并被吸收,成为漫反射光照。
- 金属表面上所有折射光都会被直接吸收而不会散开,因此金属表面不会显示出漫反射颜色。
- 折射光与反射光二者是互斥的关系。能量总和永远不会超过入射光线的能量。
反射率方程
- 反射率方程是PBR中一种渲染方程的特化版本
- 反射率方程:$L_0(p,\omega_0) = \int _\Omega f_r(p,\omega_i,\omega_0)L_i(p,\omega_i)n·\omega_i d \omega_i$
- $L$是辐射率,用来量化单一方向上发射来的光线的大小和强度
- 辐射通量$\Phi$:一个光源输出的能量,以瓦特为单位,可以视为这个光源中包含的所有波长的一个函数。
- 立体角:三位立体空间中的角度,可以描述为投射到单位球体上的截面大小。
- 辐射强度:单位球面上,一个光源向每个单位立体角所投放的辐射通量。计算公式: $I=\frac{d\Phi}{d\omega}$。
- 辐射率L:一个拥有辐射强度的光源在单位面积A,单位立体角上辐射出的总能量。也就是:$L=\frac{d^2\Phi}{dAd\omega cos\theta}$ 。如果把立体角和面积看作无穷小,就可以用辐射率来表示单束光线穿过空间中一个点的通量。
- 反射率方程$L_0(p,\omega_0) = \int _\Omega f_r(p,\omega_i,\omega_0)L_i(p,\omega_i)n·\omega_i d \omega_i$中:
- $L_i(p,\omega_i)$表示通过无限小的立体角(可以近似看作一个入射方向向量)投射到点p上的光线总和。
- $n·\omega_i$也就是余弦值$cos\theta$。
- $\omega_0$表示观察方向,也就是光线的出射方向。
- $L_0(p,\omega_0)$表示了从$\omega_0$方向上观察时,光线投射到点p上之后反射出来的辐照度
- $\Omega$表示以点p为球心,以平面法向n为轴所环绕的半球体。为
- $d \omega_i$积分元,在计算中按照一定的步长对反射率方程离散求解。
- $f_r(p,\omega_i,\omega_0)$为双面反射分布函数,也就是BRDF,它的作用时基于表面材质属性来对入射辐射度进行缩放和加权
BRDF
输入参数:入射光方向,出射光方向$\omega_0$,平面法向$n$,表示微平面粗糙程度的参数$\alpha$
当平面为理想镜面时,BRDF只对符合反射定律(即入射光、出射光、平面法向在同一平面,入射角等于出射角)的出射方向返回值为1,其他方向返回值都为0。
Blinn-Phong模型也可以认为是一个BRDF,但他不能保证能量守恒,因此不是基于物理的渲染。
Cook-Torrance BRDF(包括漫反射和镜面反射两部分):
$f_r = k_d f_{lambert} + k_s f_{cook-torrance}$
$k_s$表示入射光线中被折射部分的比例, $k_d$表示入射光线中被反射部分的比例。
漫反射部分:$f_{lambert} = \frac{c}{\pi}$ ,其中$c$表示表面的颜色。
镜面反射:$f_{cook-torrance} = \frac{DFG}{4(\omega_0·n)(\omega_i·n)}$
- $D$:正态分布函数估算在当前的表面粗糙度下,取向方向与中间向量一致的微平面的数
量。 - $G$:几何函数
描述了微平面自成阴影的属性,当平面较粗糙时,微平面可能会互相遮挡从而减少表面所反射的光线。 - $F$:菲涅尔方程
描述不同表面角下表面所反射的光线所占比例
- $D$:正态分布函数估算在当前的表面粗糙度下,取向方向与中间向量一致的微平面的数
正态分布函数
- 也称为镜面分布,从统计学上近似地表示了与某向量(一般是中间向量h)取向
一致的微平面的比例。 - 计算公式:$NDF_{GGXTR}(n.h,\alpha) = \frac{\alpha^2}{\pi((n·h)^2 (\alpha_2-1) + 1)^2}$
- 其中:$h$表示中间向量, $\alpha$表示表面粗糙度
几何函数
从统计学上近似求得微平面之间相互遮挡的比例,这种遮挡会损耗光线能量。
计算公式:$G_{SchlickGGX}(n,v,k) = \frac{n·v}{(n·v)(1-k)+k}$
其中,$k$是粗糙度$\alpha$的重映射
- 针对直接光照:$k_{direct} = \frac{(\alpha+1)^2}{8}$
- 针对IBL(image based lighting,一种间接光照技术)光照:$k_{IBL} = \frac{\alpha^2}{2}$
微平面相互遮挡包括:
- 观察方向上:几何遮蔽
- 光线方向上:几何阴影
同时考虑两种遮挡的几何函数计算公式:
$G(n,v,l,k) = G_{sub}(n,v,k)G_{sub}(n,l,k)$
菲涅尔方程
描述被反射的光线对比光线被折射部分所占的比例,该值会随着观察角度的不同而不同。
菲涅尔方程根据观察角度得出被反射的光线所占的百分比。
垂直观察时,任何物体和材质表面都有一个基础反射率,而如果从和法线夹角近似90度的方向观察,理论上所有的平面都能完全反射光线,因此反光会变得明显很多。
菲涅尔方程的近似解公式:$F_{Schlick}(h,v,F_0) = F_0 + (1-F_0)(1-(h·v))^5$
- 该近似只对电解质或者说非金属表面有定义,因为使用IOR计算基础反射率对导体表面并不能计算出正确结果。
- 对金属材质需要预先计算平面对法向入射的反应,然后基于相应观察叫的近似对这个值进行插值
- $F_0$:平面基础反射率,利用折射指数IOR算出,用RGB三原色来表示,因为对于道题该基础反射率一般是带有颜色的。
因为金属表面会吸收所有折射光线而没有漫反射,因此可以直接使用表面纹理来作为他们的基础反射率。
Cook-Torrance反射率方程
- 计算公式:$L_0(p,\omega_0) = \int _\Omega (k_d\frac{c}{\pi} + k_s \frac{DFG}{4(\omega_0·n)(\omega_i·n)})L_i(p,\omega_i)n·\omega_i d \omega_i$
PBR渲染管线中的纹理列表
- 反照率(Albedo):每一个金属的纹理像素,指定表面的颜色或者基础反射率
- 法线(Normal):使得我们可以逐片段值得独特的法线,制造表面的起伏感。
- 金属度(Metallic):逐个像素指定是否是金属质地。
- 粗糙度(Roughness):以纹理像素为单位指定表面的粗糙度,粗糙度数值会影响微平面统计学上的取向度。
- 环境光遮蔽(AO):为表面和周围潜在的几何图形指定了一个额外的阴影因子。
PBR渲染管线中的纹理列表(Metal/Roughness Workflow)
在本流程中,金属的反射率值和电解质的反射颜色一起被放置在Base color贴图
中。金属贴图就像一个Mask一样来区分Base color中的金属和电介质数据。
常见介电材料的F0被硬编码为0.04。
反照率(Albedo)
每一个金属的纹理像素,指定表面的颜色或者基础反射率。在色调上比较平坦,对比度低于传统的漫反射贴图。亮度范围最低不应该低于30-50sRGB,最高不应该高于240sRGB。
法线(Normal)
使得我们可以逐片段计算得到独特的法线,制造表面的起伏感。
金属度(Metallic)
金属贴图用于定义材料的哪些区域表示原始的金属,它类似于一个遮罩。0.0表示非金属,1.0表示金属。
原始金属的灰度范围在金属贴图中定义为235-255sRGB,落在此范围内的金属需要在Base color中有70%-100%的反射率范围。金属上的涂层或者污垢等远低于金属70%-100%的反射率所需要的值,因此在金属贴图低于235sRGB的范围内,可以在介电和金属反射率值之间创建适当的混合。
粗糙度(Roughness)
Roughness贴图以纹理像素为单位指定表面的粗糙度,描述了表面的不规则性,粗糙度数值会影响微平面统计学上的取向度。反射光方向会根据表面粗糙度变化,但强度保持不变。粗糙度高的表面具有范围更大看起来更暗的高光,而较光滑的表面则有范围较小而看起来更亮的高光。
黑色(0.0)表示光滑的表面,白色(1.0)表示粗糙的表面。
环境光遮蔽(AO):为表面和周围潜在的几何图形指定了一个额外的阴影因子。
Ⅱ. Part Two Bump Mapping基本原理
Bump Mapping(也叫Normal Mapping)也就是法线映射,简单的讲就是通过读取一张存储着法线信息的纹理来计算光照(而不直接简单地通过顶点法线的插值),这样可以明显增强图像的真实感。
法线贴图(Normal Map)
法线贴图是存储法线的一张贴图,法线的 xyz 的值经过归一化之后再被映射成为对应的 RGB 值。归一化的法线值范围为[-1,1],而RGB的每一个分量为无符号的8位组成,范围为[0,255]。即法线的分量需要从由[-1,1]映射成[0,255]。法线贴图一般呈蓝色,因为大多数朝向 (0, 0, 1) 的法线被映射成为了 (0, 0, 255)。
切空间及其变换矩阵
我们需要注意的是,法线贴图中储存的法线是在切空间中的法线值。切空间是在某一点由顶点法向和切向量组成的线性空间。在模型每个顶点中,都存在这样的一个切空间坐标系,以模型顶点为中心,以TBN三个方向分别为为3个轴(Tangent,Binormal,Normal)。其中,N是顶点的法线方向,T、B两个向量是顶点切平面的2个向量,一般T的方向是纹理坐标u的方向,B的方向(副切线方向)通过TN叉乘计算得到。
从切空间到模型空间的变换矩阵,由T、B、N三个向量组成,也叫TBN矩阵。Tangent,Binormal,Normal三个向量中,我们在模型顶点中已知Tangent和Normal的值,则Binormal可以通过前2个向量的叉乘来取得。特别的,我们需要首先将Tangent进行Gram-Schmidt向量正交化,使之与法线垂直。
Normal Mapping主要流程
因此,我们进行Normal Mapping的主要流程就是:
- 根据顶点的Normal和Tangent计算TBN矩阵
- 根据顶点UV从Normal Map采样,并将其映射回到[-1,1],从而得到切空间下的法线信息。
- 使用TBN矩阵将法线信息变换到模型空间
- 进行后续的光照计算(或许需要对法线做进一步变换转换到世界空间)
Ⅲ. Part Three Shadow Map基本原理
(本部分由于是课堂学习内容,因此在此不再赘述,只描述基本原理。)
阴影图(Shadow Map)算法是渲染时用于计算阴影的算法,也是现在使用最为广泛的阴影计算方法。
Shadow Map算法计算阴影的基本原理是:从光源可以看到场景中所有的被光照亮的表面。在光源方向不可见的表面都处于阴影区域。
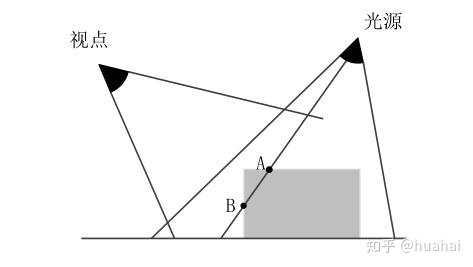
为了判断Fragment是否对于光源是可见的,需要分三步:
以光源的位置作为视点,对场景进行一次渲染,这次绘制不会将着色显示在屏幕上,而只取深度信息,得到一张深度图Shadow Map。这张纹理上的每一个像素都记录了第一个可见表面的深度值(也就是与光源的距离)。
从真实的视点对场景进行渲染,在渲染的过程中,逐片元进行矩阵变换,求出当前片元在光源为视点的空间下的深度值和UV值(也就是xy坐标值)。
使用xy坐标值从第一步生成的Shadow Map中采样,并与当前片元深度值比较。如果当前深度值大于采样得到的深度值,则证明当前片元应该是阴影,反之则证明当前片元可以被光源照亮。
其中,第一步中以光源为视点进行渲染时,如果使用的是平行光则应该采用正交投影,如果使用的是点光源则应该采用透视投影。
使用上述方法得到的阴影会有明显的锯齿状,因此在项目中我还使用了老师上课介绍的PCF算法,以期望得到软阴影,柔化阴影边缘,消除锯齿状走样。
- PCF方法的主要原理是,在从Shadow Map采样时,不仅采样当前UV,还要采样周围的像素(比如一个以当前UV为中心的3*3的窗口),将当前片元的深度值分别与这个窗口内的每一个深度值比较,如果大于当前片元深度值就取值为1,否则取值为0。之后再对这样得到的一个由0和1组成的窗口进行卷积操作(一般是求平均),从而得到当前片元的阴影系数,这样就实现了软阴影。
Ⅳ. Part Four 模型处理及贴图烘焙
对模型的预处理:
- 使用Maya对模型的大小和旋转方向做了预先处理,这部分在代码里实际上也能通过ModelMatrix来实现,但是由于加入了其他的模型(比如点光源、背景幕布),为了统一,便使用了在Maya中预先处理好的方法。


- 两个模型的人体部分是硬边,也就是每个顶点有多个法线,这样会使得最终的渲染效果皮肤表面有棱角,不够平滑,因此我对两个模型的身体部分在Maya中进行了软化边操作。(下图展示软化边操作前后的模型效果及顶点法线)




如上图,没有做软化边的模型每个顶点有多个法线,软化边之后的模型每个顶点只有一个法线
自行建模得到了一个幕布,并同样为其制作贴图,对其进行PBR流程渲染。(见上图)
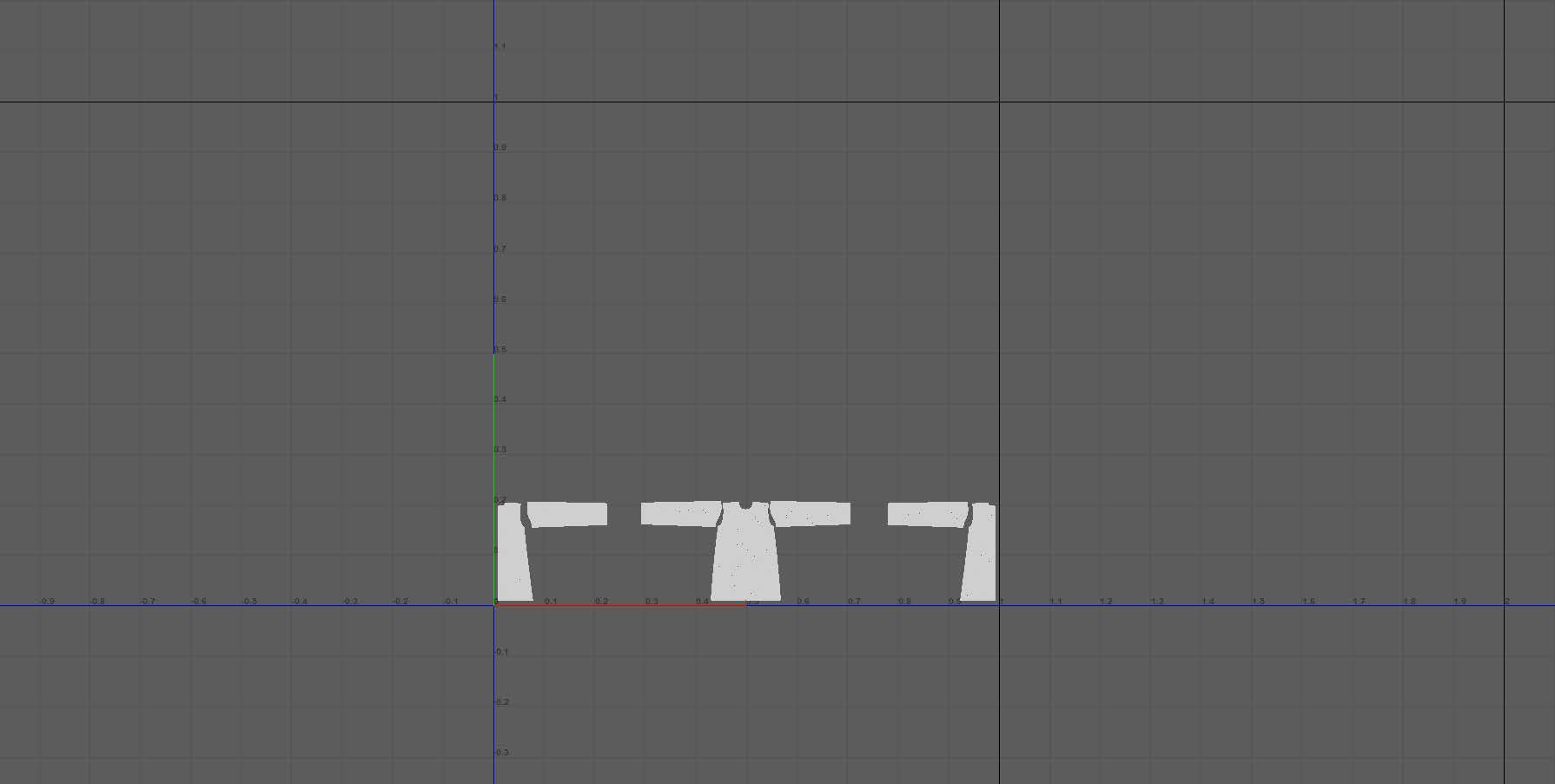
有些模型的UV没有展开(比如身体部分),对这些模型进行了UV自动展开(因为皮肤部分对UV排布方式的要求不高)
其他模型(衣物等)虽然有展开好的UV,但是该UV并没有在0-1的范围内,因此使用Maya将该展开后的UV放在0-1之内的范围内。

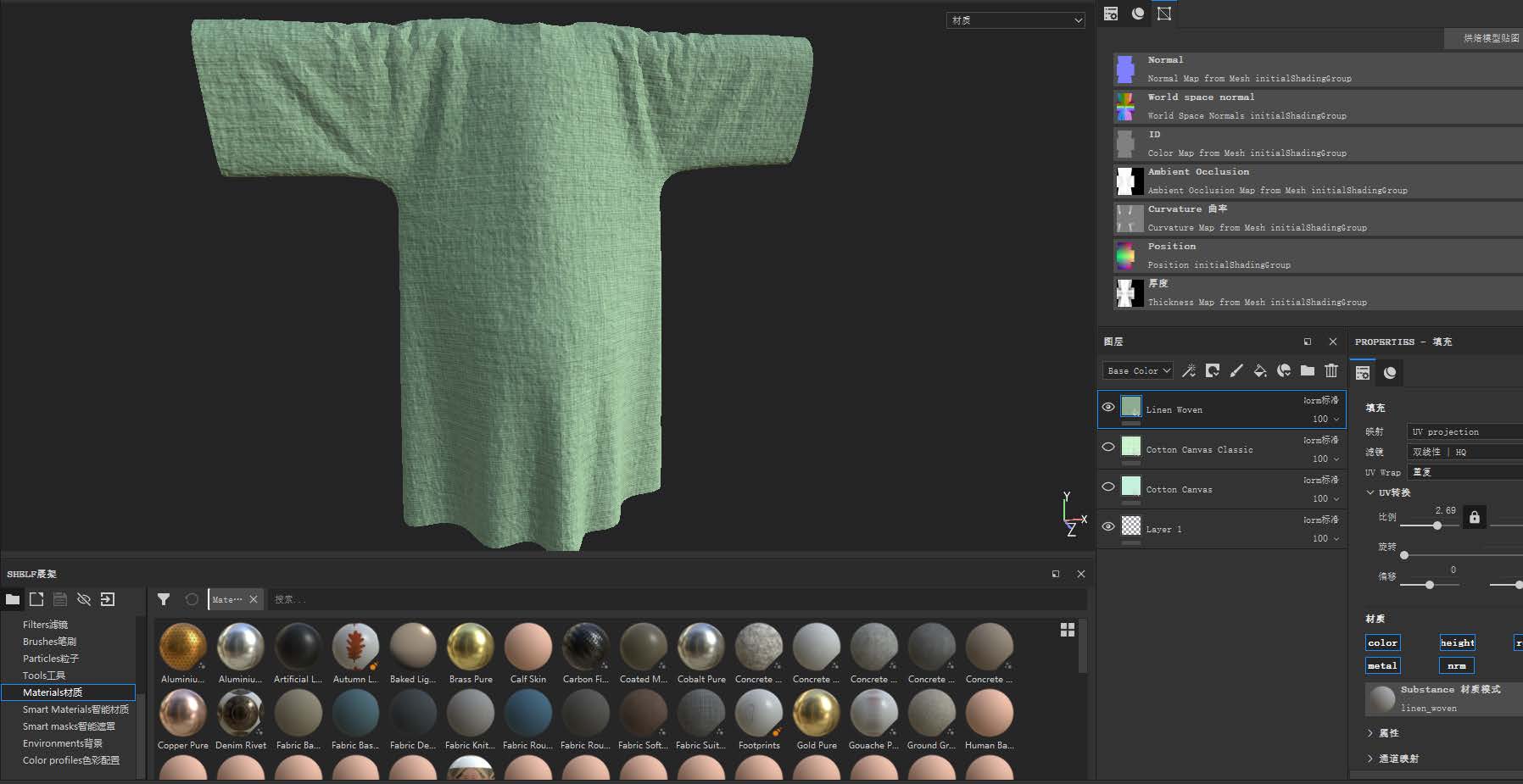
贴图的烘焙制作:
- 自行使用Substance Painter完成模型贴图的制作,PBR流程中导出的贴图有Albedo、Normal Map、Metallic Map、Roughness Map、Height Map五张。其中每个模型都使用的有Albedo、Normal Map、Roughness Map。由于本次渲染实验中没有模型有金属度,因此所有的Metallic Map都是一张黑色贴图,可以直接不添加该帖图,Shader会自动使用默认值0。另外,本次实验中也暂时没有烘焙和使用AO贴图。


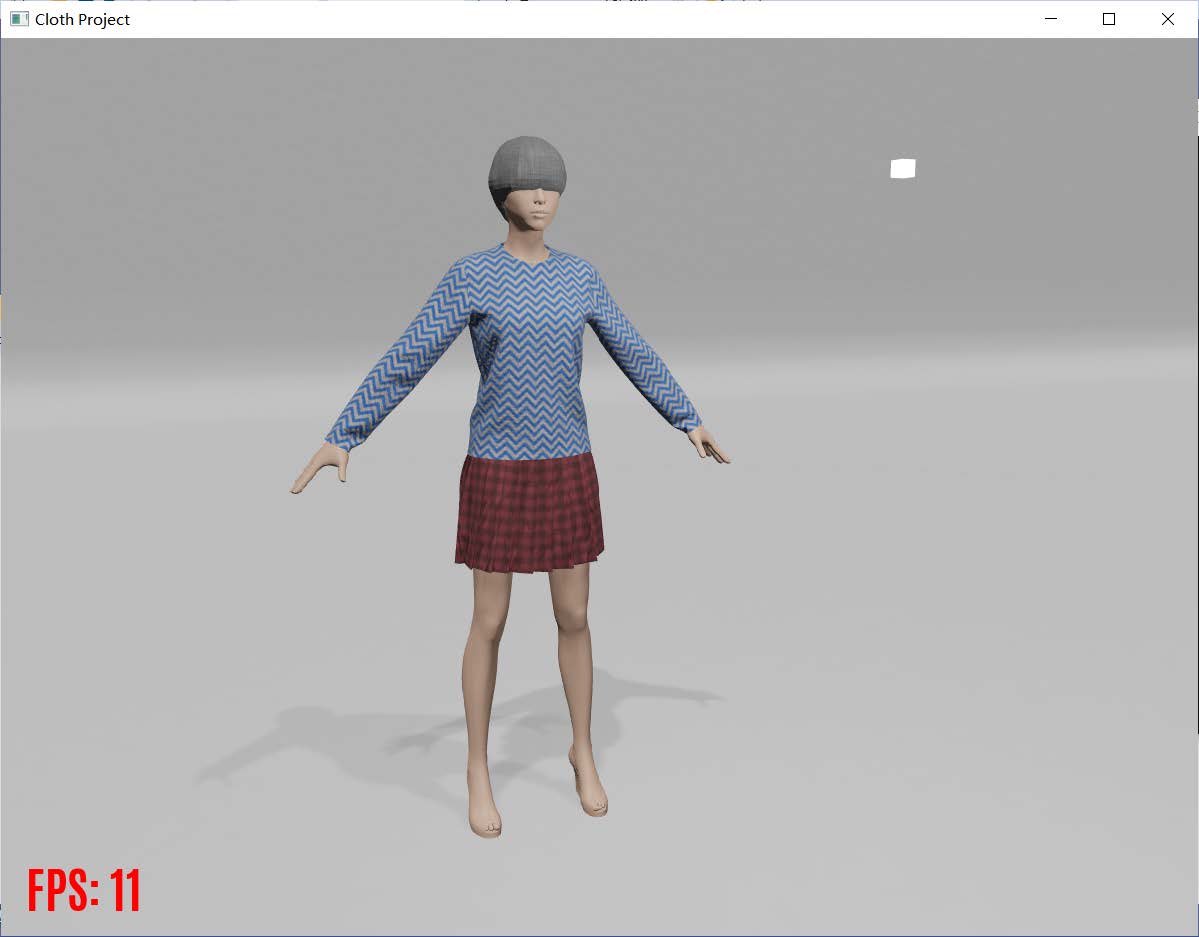
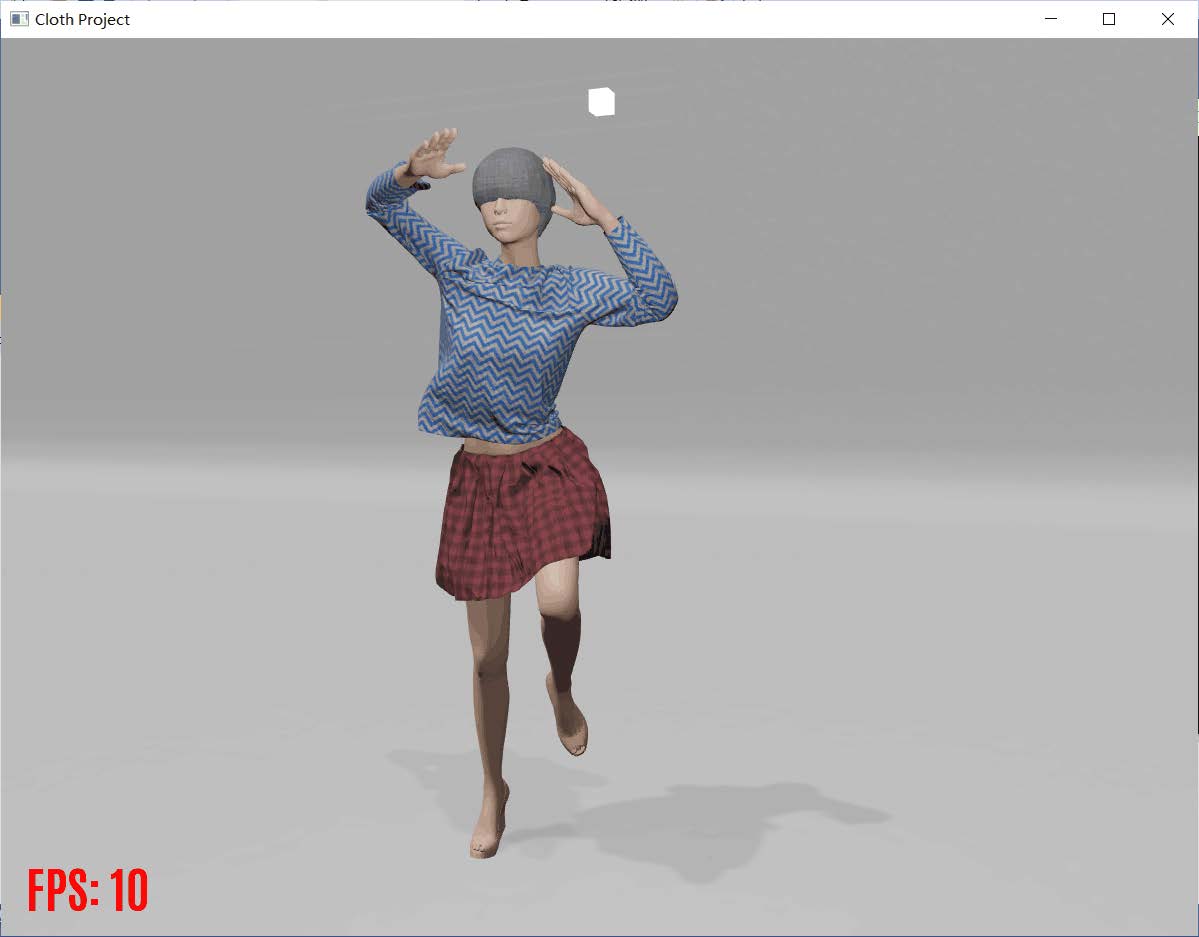
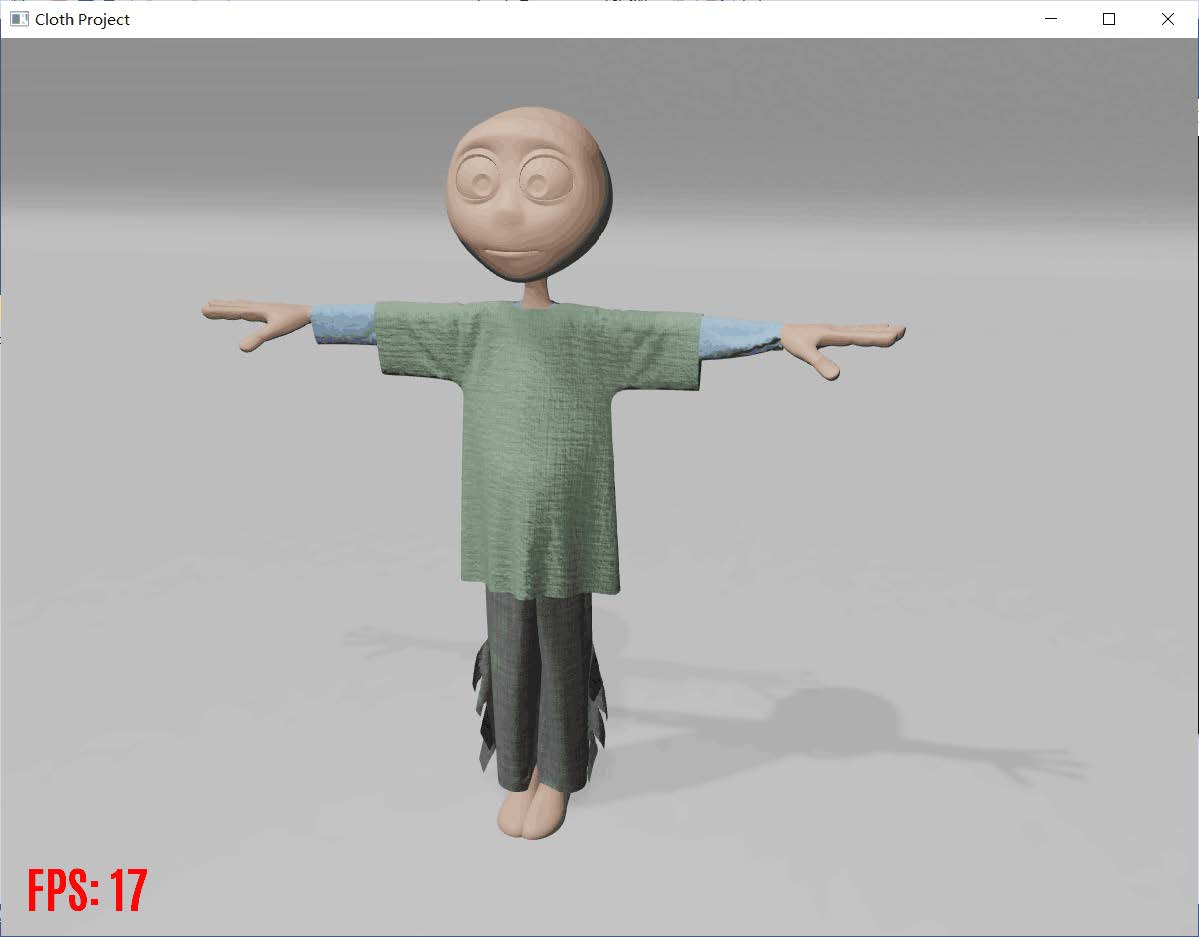
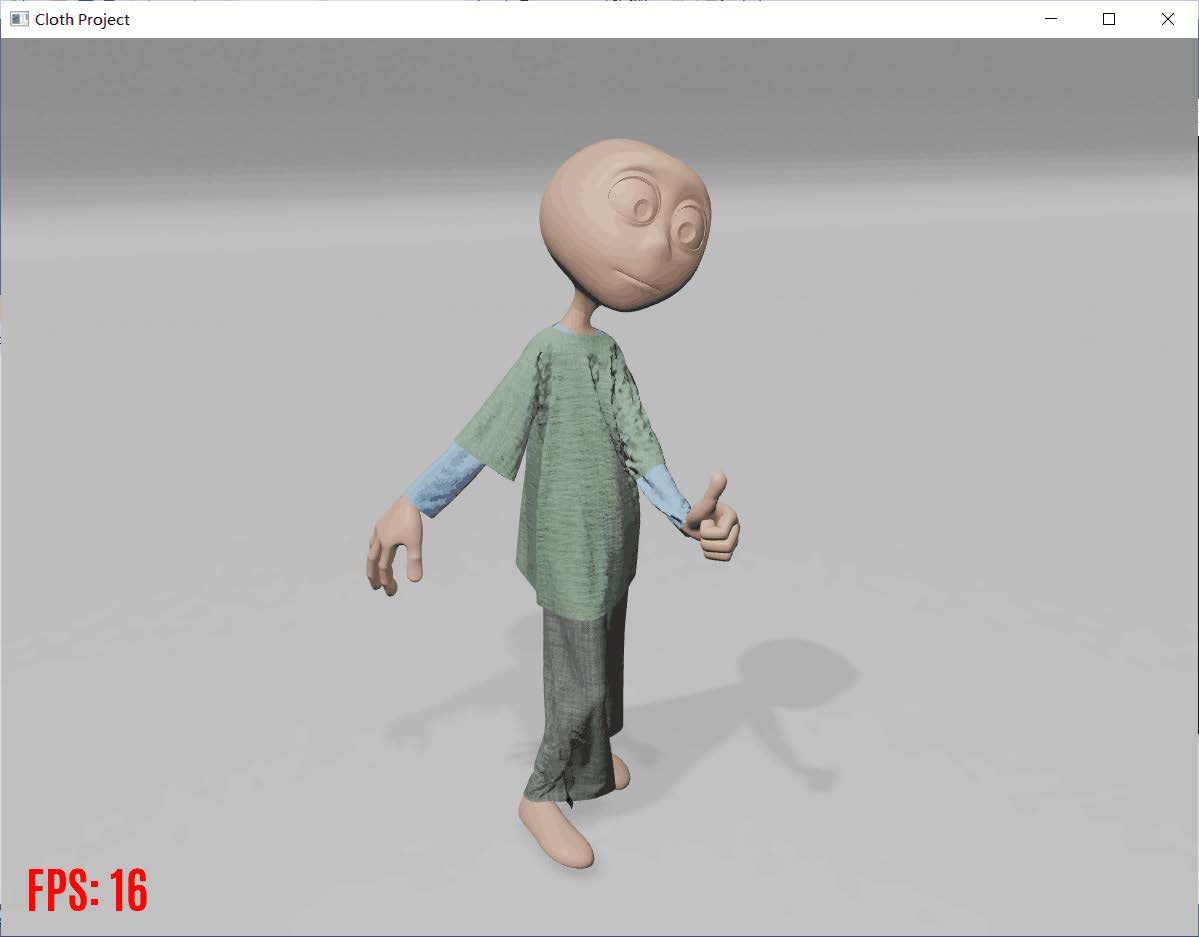
Ⅴ. Part Five 效果展示
工程运行效果可以查看”录屏展示“文件,本处展示一些运行截图。(截图效果可能因为截图软件分辨率不够等因素,效果并没有直接看的好。)由于设备显卡比较陈旧,渲染FPS似乎较低。