计算机视觉HW3 - Harris角点检测

课程名称：计算机视觉
实验项目名称：harris角点检测
实验日期：2020 年 12 月 16 日

一、实验目的和要求

• 读入摄像头，回放视频。按一下空格键，则暂停回放，并将当前帧图像做 Harris Corner 检测 ，并将检测的结果叠加在原来图像上。
  1.需要自己写代码实现 Harris Corner 检测算法，不能直接调用OpenCV 里面与 Harris 角点检测相关的函数；
  2.显示中间的处理结果及最终的检测结果，包括最大特征值图、最小特征值图、R 图 、原图上叠加检测结果等，并将
  这些中间结果都输出保存为图像文件。

二、实验原理

本实验中主要使用了 Harris 角点检测算法(Harris Corner Detection)。

1）算法简介

匹配问题

Harris角点检测是Chris Harris和Mike Stephens在1988年提出的。主要用于运动图像的追踪。当时的普遍想法是利用边缘进行追踪，但边缘匹配很难达到预期的效果。即使是当时最优秀的边缘检测算子Canny算子，它的边缘检测也依赖于阈值的选取。所以Harris等人放弃了匹配边缘，转而寻找一些特殊的点来匹配，这些点是边缘线段的连接点，它们表征了图像的结构，代表了图像局部的特征。

什么是角点

直观的说就是图像轮廓的连接点。不管视角怎么变换，这些点依然存在，是稳定的；它们与领域的点差别比较大。所以角点是一种优良的特征点。

角点往往是两条边缘的交点，它是两条边缘方向变换的一种表示，因此其两个方向的梯度变换通常都比较大并且容易检测到。

Harris角点检测是通过数学计算在图像上发现角点特征的一种算法，而且其具有旋转不变性的特质。

OpenCV中的Shi-Tomasi角点检测就是基于Harris角点检测改进算法。

2）基本原理

人们通常通过在一个小的窗口区域内观察点的灰度值大小来识别角点，如果往任何方向移动窗口都会引起比较大的灰度变换那么往往这就是我们要找的角点。角点是一幅图像上最明显与重要的特征，对于一阶导数而言，角点在各个方向的变化都比较大，而边缘区域在只是某一方向有明显变化。一个直观的图示如下：

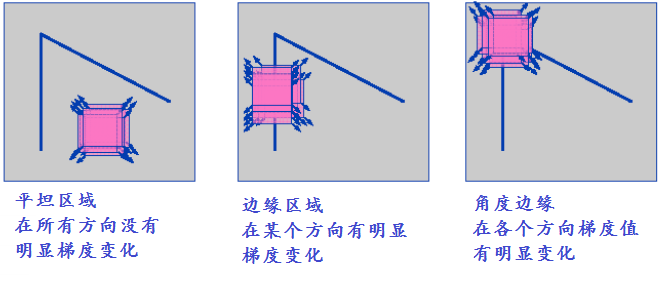
3） 数学原理

基本数学公式如下：
$$
E(u,v)=\sum _{x,y} w(x,y)[I(x+u,y+v)-I(x,y)]^2
$$

其中$I(x, y)$表示像素灰度值强度，范围为0～255，$W(x, y)$表示移动窗口窗函数，可以是加权函数，也可以是高斯函数。

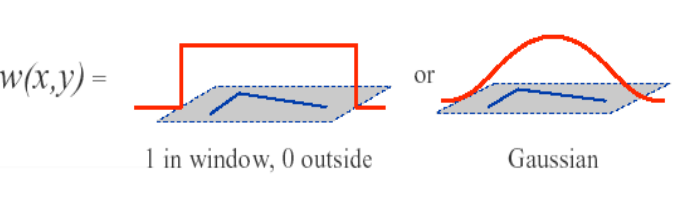
对 $f(x,y)$ 进行二维泰勒展开：

略去二阶及更高阶项，上式可近似为：
$$
f(x+u,y+v) \approx f(x,y)+uf_x(x,y)+vf_y(x,y)
$$
于是对于$E(u,v)$，我们有以下的推导：

对于较小的位移，$E(u,v)$ 可以近似为：
$$
E(u,v) \simeq \begin{bmatrix} u & v \end{bmatrix} M\begin{bmatrix} u \v \end{bmatrix}
$$

其中M为：
$$
M=\sum_{x,y}w(x,y) \begin{bmatrix} I_x^2 & I_xI_y \I_xI_y & I_y^2 \end{bmatrix}
$$

二次项本质上可以看成一个椭圆函数，矩阵M有特征值$\lambda_1 ,\lambda_2$，如下图，根据 $\lambda_1 ,\lambda_2$ 的值我们可以把其分为三类：

1. λ1，λ2都很小且近似，E在所有方向接近于常数；

2. λ1>>λ2,或者λ2>>λ1, E将在某一方向上较大，其他方向较小；

3. λ1，λ2都很大且近似，E将在所有方向上都较大；

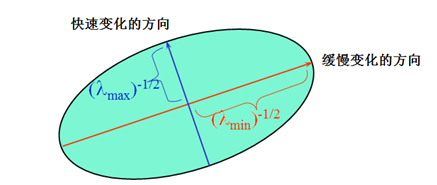
如下图，上述三种情况，分别对应图像中的：

1. 变换不大，较为平缓的部分
2. 边缘
3. 角点

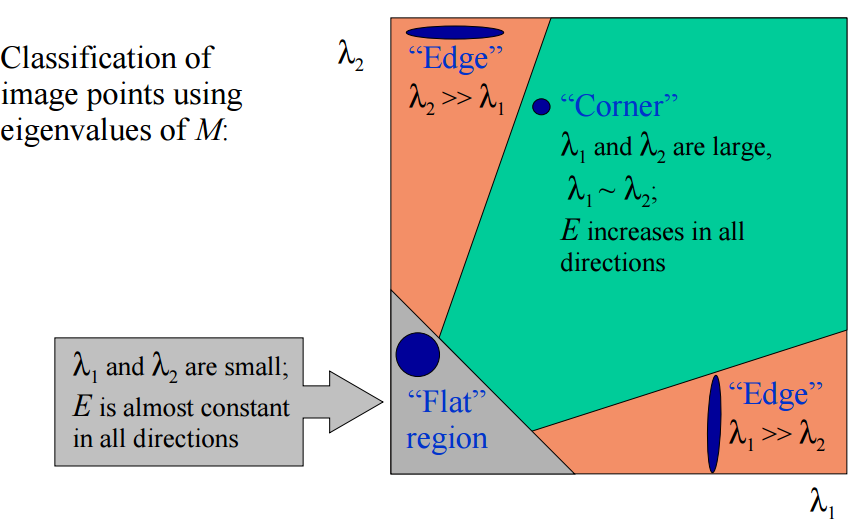
最后我们通过计算角点响应值R来判断其属于哪个区间，也就是属于平缓区，边缘，还是角点：
$$
R=detM - k (trace M)^2
$$

$$
其中，det M = \lambda_1 \cdot \lambda_2　　　　trace M=\lambda_1 + \lambda_2
$$

其中k一般为常数，一半取在0.04~0.06。

4）算法详细步骤

1. 计算图像X方向与Y方向的梯度也就是一阶偏导数： $I_x , I_y$

$$
I_x=G_{\sigma}^x * I　　I_y=G_{\sigma}^y * I
$$

2. 根据第一步的结果计算每个像素点的梯度平方： $I_x^2,I_y^2,I_xI_y$

$$
I_x^2=I_x \cdot I_x　　I_y^2=I_y \cdot I_y　　I_xI_y=I_x \cdot I_y
$$

3. 高斯模糊第二步三个值得到Sxx, Syy, Sxy

$$
S_{xx}=G_{\sigma’}*I_{x}^2　　S_{yy}=G_{\sigma’}*I_{y}^2　　S_{xy}=G_{\sigma’}*I_x I_y
$$

4. 定义在每个像素点的矩阵H，也就是前面的M矩阵

$$
H(x,y)=\begin{bmatrix} S_{xx}(x,y) & S_{xy}(x,y) \ S_{xy}(x,y) & S_{yy}(x,y) \end{bmatrix}
$$

5. 计算每个像素的角点响应值R

$$
R=Det(H)-k(Trace(H))^2
$$

6. 设置阈值找出可能点并进行非极大值抑制

三、实验内容和过程分析

1）实现从摄像头读入视频并回放，以及根据按键进行不同的操作。

读入摄像头，回放视频。按一下空格键，则暂停回放，并将当前帧图像做一次 Harris Corner 检测 ，并将检测的结果叠加在原来图像上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

int main()
{	
	VideoCapture capture(0); //打开一个默认的相机	
	if (!capture.isOpened()) return -1; //检查是否成功打开	
	bool show = false; //是否有角点检测结果正在展示
	while (true) {
		//从相机连续读取图像
		Mat frame;
		capture >> frame;		
		Mat src = frame.clone();
		if (!src.data) return -1;
		imshow("video", src);

		int c = waitKey(30);
		//空格键操作
		if (c == 32)
		{
			if (!show) {  //按下空格键后会对当前帧图像做角点检测
				string addr_pre=Harris(src, 0.05, 0.001);
				imshow("result", src);
				imwrite(addr_pre + "Result.png", src);
			}
			else {  //如果当前已经有角点检测结果窗口在展示, 则按空格关闭展示窗口
				destroyWindow("corner");
				destroyWindow("max");
				destroyWindow("min");
				destroyWindow("result");
				destroyWindow("R");
			}
			show = !show;	
		}
		else if (c == 'q' || c == 'Q'|| c==27)  //按Q/q或者Esc键关闭结果展示窗口
		{
			destroyWindow("corner");
			destroyWindow("max");
			destroyWindow("min");
			destroyWindow("result");
			destroyWindow("video");
			destroyWindow("R");
			return 0;
		}
	}
	return 0;
}

2）Harris Corner Detection

1. 计算图像X方向与Y方向的梯度也就是一阶偏导数： $I_x , I_y$

$$
I_x=G_{\sigma}^x * I　　I_y=G_{\sigma}^y * I
$$

2. 根据第一步的结果计算每个像素点的梯度平方： $I_x^2,I_y^2,I_xI_y$

$$
I_x^2=I_x \cdot I_x　　I_y^2=I_y \cdot I_y　　I_xI_y=I_x \cdot I_y
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

//转灰度图
Mat gray;
cvtColor(I, gray, CV_BGR2GRAY);

//计算图像X方向与Y方向的一阶偏导Ix、Iy以及Ix^2,Iy^y,IxIy
Mat IxIx(gray.rows, gray.cols, CV_32FC1);
Mat IyIy(gray.rows, gray.cols, CV_32FC1);
Mat IxIy(gray.rows, gray.cols, CV_32FC1);

//初始化为0 (此部分在报告中省略)

//计算偏导数及Ix^2,Iy^y,IxIy
for (int y = 1; y <= I.rows - 2; y++){
    for (int x = 1; x <= I.cols - 2; x++){
        float ix = (float)gray.at<uchar>(y + 1, x) - (float)gray.at<uchar>(y - 1, x);
        float iy = (float)gray.at<uchar>(y, x + 1) - (float)gray.at<uchar>(y, x - 1);

        IxIx.at<float>(y, x) = (float)ix * (float)ix;
        IyIy.at<float>(y, x) = (float)iy * (float)iy;
        IxIy.at<float>(y, x) = (float)ix * (float)iy;
    }
}

3. 高斯模糊第二步三个值得到Sxx, Syy, Sxy

$$
S_{xx}=G_{\sigma’}*I_{x}^2　　S_{yy}=G_{\sigma’}*I_{y}^2　　S_{xy}=G_{\sigma’}*I_x I_y
$$

1
2
3
4
5
6
7
8
9

//计算图像X方向与Y方向的一阶偏导Ix、Iy以及Ix^2,Iy^2,IxIy
Mat Sxx(gray.rows, gray.cols, CV_32FC1);
Mat Syy(gray.rows, gray.cols, CV_32FC1);
Mat Sxy(gray.rows, gray.cols, CV_32FC1);

//高斯滤波
GaussianBlur(IxIx, Sxx, Size(5, 5), 0, 0);
GaussianBlur(IyIy, Syy, Size(5, 5), 0, 0);
GaussianBlur(IxIy, Sxy, Size(5, 5), 0, 0);

4. 定义在每个像素点的矩阵H，也就是前面的M矩阵

$$
H(x,y)=\begin{bmatrix} S_{xx}(x,y) & S_{xy}(x,y) \ S_{xy}(x,y) & S_{yy}(x,y) \end{bmatrix}
$$

5. 计算每个像素的角点响应值R

$$
R=Det(H)-k(Trace(H))^2
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

//R值和最大最小特征值矩阵
Mat R(gray.rows, gray.cols, CV_32FC1);
Mat Max(gray.rows, gray.cols, CV_32FC1);
Mat Min(gray.rows, gray.cols, CV_32FC1);
//最大响应值Rmax
float maxResponse = 0.0f;

//初始化为0 （此部分在此省略）

//计算最大最小特征值以及harris响应值R
for (int y = 0; y <I.rows; y++) {
	for (int x = 0; x <I.cols; x++) {			
		float aa = 0;
		float bb = 0;
		float cc = 0;
		aa = Sxx.at<float>(y, x);
		bb = Syy.at<float>(y, x);
		cc = Sxy.at<float>(y, x);

		//计算当前像素的harris响应值
		float t = (aa * bb - cc * cc) - k * (aa + bb) * (aa + bb);
		
		//计算最大最小特征值
		float po1 = pow(1.0 * aa - bb, 2);
		float po2 = 4.0 * cc * cc;
		float sq = sqrt((double)(po2 + po1));
		float max = 0.5 * (aa + bb + sq);
		float min = 0.5 * (aa + bb - sq);

		R.at<float>(y, x) = t;
		Max.at<float>(y, x) = max;
		Min.at<float>(y, x) = min;

		//记录最大响应值
		if (t > maxResponse)
			maxResponse = t;
	}
}

6. 设置阈值找出可能点并进行非极大值抑制

1
2
3
4
5
6
7
8
9
10
11
12
13

Mat localMax; 
//进行局部非最大值抑制
localMaxFilter(R, localMax, max_size);

//剔除部分局部极大值
Mat Corner=localMax;
threshold(localMax, Corner, thres_hold * maxResponse, 255, THRESH_BINARY);

//在原始图像上绘制角点检测结果
for (int y = 0; y < Corner.rows - 1; y++)
	for (int x = 0; x < Corner.cols - 1; x++)
		if (Corner.at<float>(y, x))
			circle(I, Point2i(x, y), 2, Scalar(255, 242, 0));

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

//非局部极大值抑制
void localMaxFilter(Mat& in, Mat& out, int size=3)
{
    Mat dilated;
    dilate(in, dilated, Mat()); //对输入进行膨胀操作
    if (out.empty())
        out.create(in.rows, in.cols, in.type());

    for (int y = 0; y < in.rows; y++) {
        for (int x = 0; x < in.cols; x++) {
            //如果像素点的值和膨胀操作前相同，证明该点为局部极大值点
            if (in.at<float>(y, x) == dilated.at<float>(y, x))
                out.at<float>(y, x) = in.at<float>(y, x);
            else
                out.at<float>(y, x) = 0.0f;
        }
    }
}

四、实验结果展示

1）使用本地图像检测Harris Corner Detection效果

1. 原图

2. 最大特征值图

3. 最小特征值图
   

4. 响应值R图
   

5. 角点检测结果
   

6. 角点检测结果与原图叠加
   

7. 原图
   

8. 最大特征值图
   

9. 最小特征值图
   

10. 响应值R图
    

11. 角点检测结果
    

12. 角点检测结果与原图叠加
    

五、实验思考和感想

​ 通过本次实验，我更加深入地学习和体会了Harris角点检测的算法，在实践的过程中，我发现了很多在学习过程中没有注意到的细节，都需要在实践进行调整。

​ 在实验初期，调整角点检测的R值阈值给我造成了一定的困扰，对于不同的图像，似乎需要不同的阈值，才能得到较为合理较为优秀的结果，后期，我发现这个阈值由于是一个绝对值，而图像的性质不同会使得R值的范围变化非常大，因此，我将这个阈值设置成为一个函数，在计算图像中每个像素点的R值时，记录下最大的R值，在后续的处理中，以关于这个最大值的一个比例函数，例如K*MaxValue，作为选择角点的阈值，这样处理之后，算法对于不同图像的适应度增强了很多，但由于只获取了最大R值的信息，因此还是不能完全做到自适应，在某些情况下需要对阈值函数进行微调。

​ 在实验中，我还发现，计算R值和最大最小特征值时，由于结果数据可能溢出八位，因此不能再采用位深度为8的图像格式变量，因此，我将图像深度改为了32位，float类型，才得以储存原始数据。

​ 由于实验需要要求保存进行角点检测的中间结果，且我在本次试验中实现了可以进行通过空格键在一次程序运行期间进行多次的角点检测（具体操作方式见ReadMe），因此我调用了函数，在每次进行角点检测时，得到系统时间，转化成字符串，作为图像输出文件名前缀，后缀则代表着该图像的属性，如Max代表该图像是最大特征值图，Corner代表该图像是得到的角点检测结果图。