在当前的图形学前沿研究中,对人脸的真实感渲染,基本都是基于PBR理论的。基于物理的渲染(Physically-based rendering)指的是使用数学建模的方式,模拟物体表面各种材质对光线反射和折射的特性,从而达到逼近真实的渲染效果的技术。其主要特点是遵循真实物理规律,光与材质相分离,且材质参数取自真实生活中的材质特征。由于本身基于物理原理,使用PBR的渲染效果相较于简单的Phong等模型会更加真实,其基于物理的参数设置也使得美术工作者可以对材质进行可预见效果的调节。
渲染与材质息息相关,私以为如果说Rasterization Rendering Pipeline,Path Tracing是渲染的骨骼,那么Materials就是渲染的心脏,是决定Mesh表面着色,光线追踪中光线Bounce后的采样方向等重要环节的核心模块。而所谓的Physically Based Rendering,除了Path Tracing本身是Physically Based的一种想法之外,Physically Based Materials也是必不可少甚至于根本上反映Physically的一环。
我从本科学习时就曾经接触到Physically Based Rendering,但是直到做我的毕业论文课题时才对其有了一个较为全面的基础了解,但或许是我天资较差,相关的知识于我而言总是常看常新的,在至今的一两年中每次学习总是能发现自己之前理解的不对的地方,在最近做Blender和Mitsuba中材质模型的对齐工作时,我总算觉得自己对Physically Based Material有了一个自己认为还比较完整的理解,故将自毕业论文以来的学习和思考整理于此。(当然之后也可能再次进行学习并推翻现在的一些想法。
本篇的核心追求是完整地梳理PBR材质相关的知识线,因此相对来说可能会较为啰嗦,会引用一些我本科毕业论文中的原文,还望海涵。
基础概念的引入
基于物理的渲染(PBR, Physically-Based Rendering)是计算机图形学中用数学建模的方式模拟物体表面各种材质散射光线的属性从而渲染照片真实图片的技术,是近年来渲染的大趋势。它主要的特点是遵循物理规律,光与材质是分离的,且控制材质的参数是与现实生活中的材质特征对应的。
由于PBR本身基于物理原理,因此,这种渲染方式相比于之前的Phong或者Blinn-Phong这样简单的模型来说,渲染结果会更加真实。另一方面,PBR也使得美术人员可以直接以物理参数为依据来调节和编辑材质,使得材质可以有基于物理性质可预见的视觉变化,并且无论光照条件如何,这样的材质都会是相对来说物理合理的。
BRDF(Bidirectional Reflectance Distribution Function,双向反射分布函数)是真实感图形学中最核心的概念之一,是用于描述光反射现象的基本模型,描述的是入射光线经过物体表面反射后如何在各个出射方向上分布。其输出是入射光线方向和出射光线方向,并且由于都是归一化的向量,因此输入其实是四维的,输出是出射光线占入射光线的比例。而PBR中使用的BRDF模型通过包含材质的各种几何及光学性质来尽可能精确的近似现实世界中的材料,它必须满足至少如下两条特性:能量守恒、亥姆霍兹光路可逆性(Helmholtz Recoprpcity Rule)。
BRDF:Bi-directional Reflective Distribution Function
BTDF:Bi-directional Transmit Distribution Function
BSDF:Bi-directional Scattering Distribution Function
其中,BSDF中的Scattering是反射和折射的统称,实际使用时BSDF = BRDF + BTDF
微表面和Cook-Torrance模型
微表面模型(Microfacet)是PBR中的重要理论基础。该假设认为物体表面是由法线方向不同的众多微小表面组成的。目前业界大部分的实时渲染管线使用的都是Cook-Torrance BRDF模型,该模型的整体反射方程为:
$ L_o (p,ω_o )= \int_\Omega (k_d \frac{c}{π} +k_s \frac{DFG}{4(ω_o·n)(ω_i·n)} ) L_i (p,ω_i )n·ω_i dω_i $
其中BRDF也就是反射部分的公式是:
$ f(l,v)= \frac{D(h)F(v,h)G(l,v,h)}{(4(n·h)(n·v))} $
D: 法线分布函数(Normal Distribution Funtion)
在BRDF模型中,法线分布函数(Normal Distribution Function,简写为NDF),也就是上述公式中的D(h),被用来描述表面一点的所有微表面的法线分布概率。输入一个朝向h,NDF会返回朝向是h的微表面占所有微表面的比例。
在微表面模型的假设下,表面越粗糙,每个微面将沿着表面排列得越混乱,从而导致方向范围更广泛的镜面反射。相反,在光滑的表面上,光线更有可能沿大致相同的方向反射,从而产生更小、更清晰的反射。
理论上来讲,微表面可以通过几何上的面片进行模拟,但是由于这些微面过于小,我们无法在每个像素的基础上区分它们,因此在基于物理的渲染工作流中,业界一般使用的方法是:在给定粗糙度参数的情况下,在统计上近似这些微平面。通过对粗糙度贴图(Roughness)采样,以计算微平面归一化的法线分布函数,可以将需渲染的几何体细化到了微观尺度(Microscale)的亚像素层面,所以能够带来更加接近真实的渲染质量和更全面的材质外观质感把控。也就是说,Roughenss Map其实是亚像素级别的 Normal Map。
NDF函数有许多不同的模型,按照提出的时间可以总结为(本总结摘自毛星云大佬的知乎文章):
- Berry[1923]
- Beckmann[1963]
- Phong [1973]
- Blinn-Phong[1977]
- ABC[1989]
- GGX[2007]
- Trowbridge-Reitz[1975]
- Shifted
- Gamma Distribution
- SGD[2012]
- Trowbridge-Reitz(GTR)[2012]
- Student’s T-Distribution STD[2017]
- Exponential Power Distribution
- EPD[2017]。
其中目前业界最常使用的是由 Bruce Walter 和 Kenneth Torrance提出的GGX NDF和Beckmann NDF。
- GGX的公式:
$ NDF_{GGXTR} (n,h,α)= \frac{α^2}{(π((n·h)^2·(α^2-1)+1)^2 )} $ - Beckmann公式:
$ NDF_{Beckmann} (n,h,\alpha) = \frac{1}{\pi \alpha^2 (n·h)^4} e^{(\frac{(n·m)^2-1}{\alpha^2 (n·m)^2})} $
下图是不同NDF公式的曲线可视化对比,其中红线为 $α_b=0.2$ 时的Beckmann-NDF,蓝线为 $α_p=48$ 时的Phong-NDF,绿线为 $α_g=0.2$ 时的GGX-NDF。从图中不难看出,GGX分布函数拥有一个比Beckmann和Phong模型更大的拖尾,衰减更慢,因此在实际使用中使用GGX会使得高光衰减过渡更自然。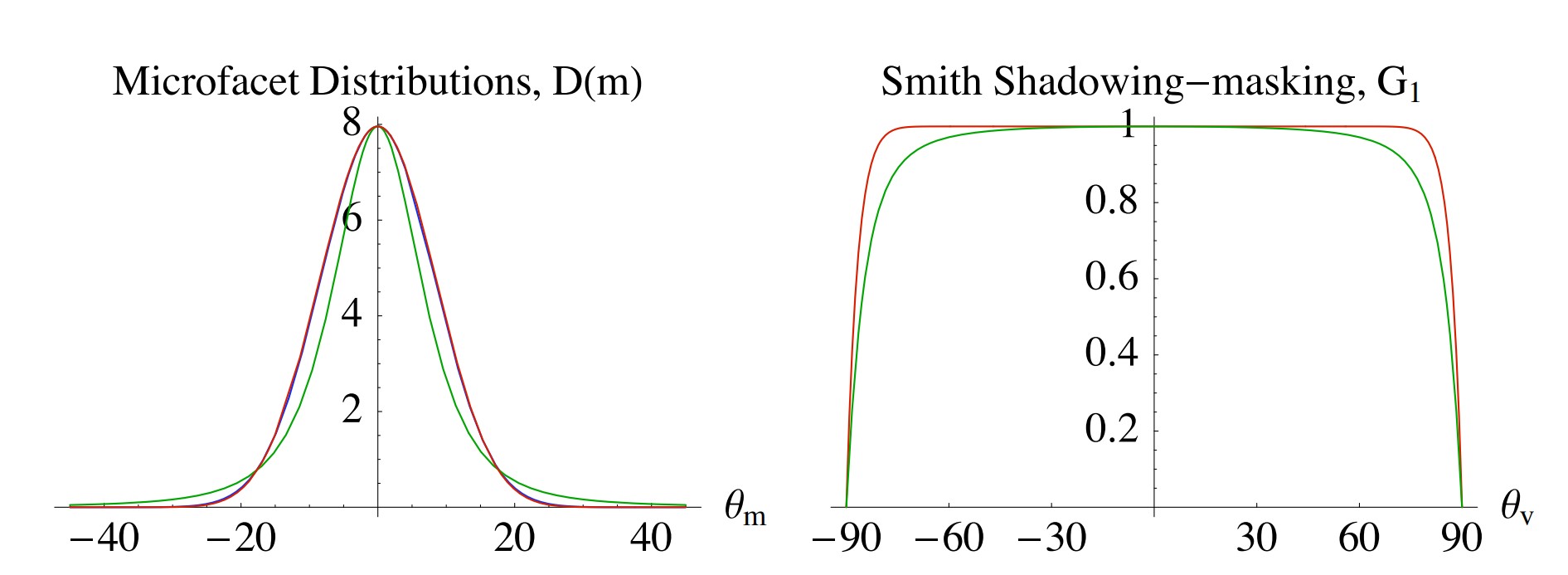

另外,Brent Burley在Physically-based shading at Disney中提出了一种叫做GTR的通用的NDF模型,其可以通过参数 γ 控制NDF曲线的形状,及其拖尾的大小,从而控制材质的光影过渡程度,当 γ 为2时等于GGX模型。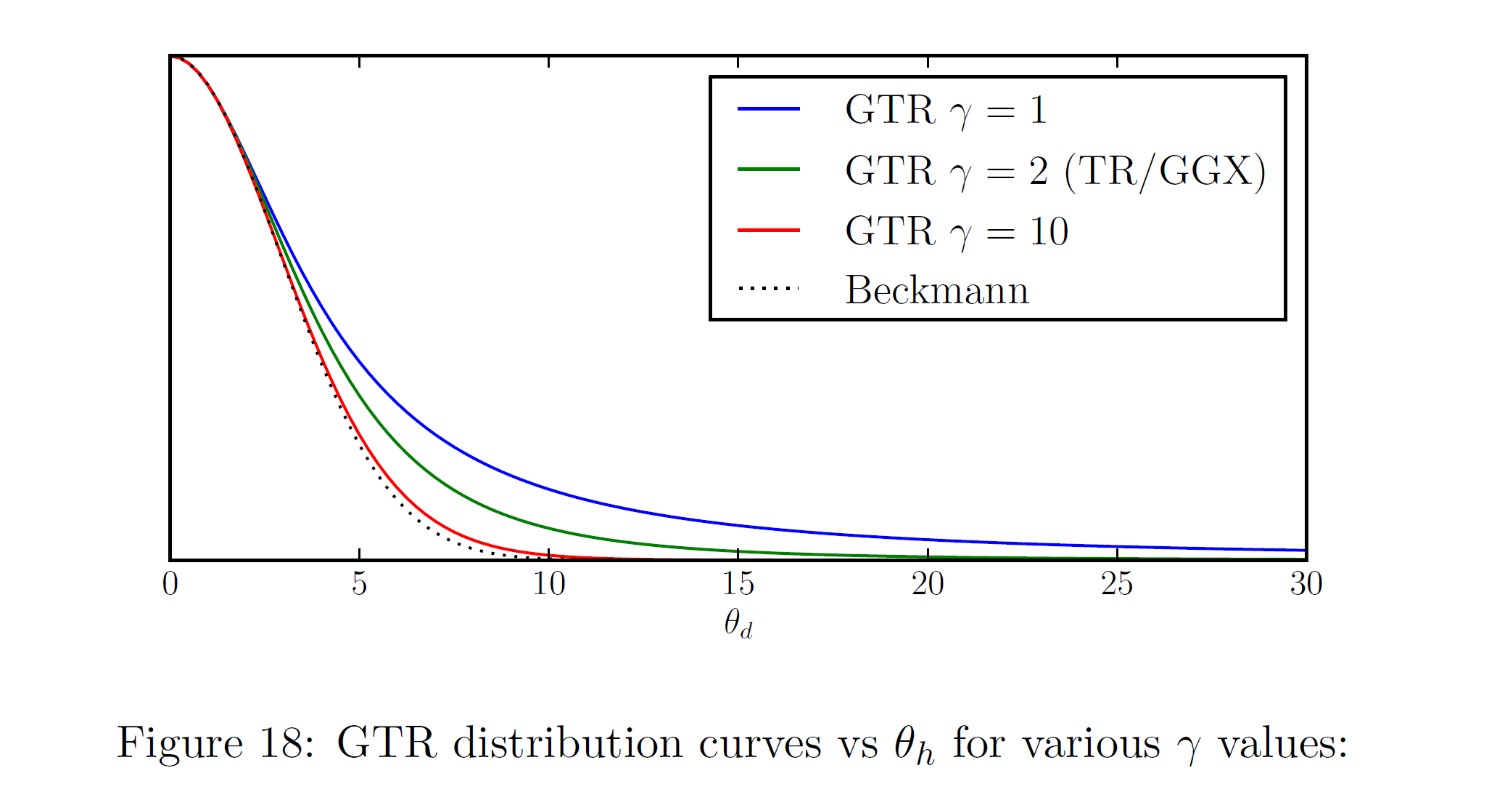
G: 几何遮蔽函数(Geometric Shadowing Function)
BRDF模型中的几何遮蔽函数是用于描述由于微表面的自阴影行为而导致的光衰减的函数。这种近似模拟了在给定点微面相互遮挡或光在多个微面上反弹的概率。在这些情况下,光在到达视点之前会失去能量,因此宏观也就表现为我们观察到该处的反射强度会降低。
几何阴影函数对于 BRDF 模型是否满足能量守恒至关重要。如果没有几何阴影函数,可能会导致物体表面反射的光比接收的更多。BRDF 方程一个关键部分是有效表面积(指的是能将光线从光源方向反射到视点方向的表面所覆盖的面积与微面表面的总表面积之间的比率)。而如果不考虑几何阴影函数,则该有效表面积可能会超过总面积,也就破坏了能量守恒。
几何阴影也有不同的拟合公式,历史上主流的几何函数建模,按提出或归纳的时间进行排序,可以总结为(摘自毛星云知乎文章):
- Smith [1967]
- V-cavity(Cook-Torrance)[1982]
- Schlick-Smith [1994]
- Neumann [1999]
- Kelemen [2001]
- Implicit [2010] [21]
其中,Smith遮蔽函数(Smith masking function)是现在业界所采用的主流遮蔽函数,Eric Heitz在2014年[4]将其拓展为Smith联合遮蔽阴影函数(Smith Joint Masking-Shadowing Function),该函数具有四种形式:
- 分离遮蔽阴影型(Separable Masking and Shadowing)
- 高度相关遮蔽阴影型(Height-Correlated Masking and Shadowing)
- 方向相关遮蔽阴影型(Direction-Correlated Masking and Shadowing)
- 高度-方向相关遮蔽阴影型(Height-Direction-Correlated Masking and Shadowing)
其中,高度相关遮蔽阴影型及其近似,是目前业界采用的主流遮蔽阴影函数。高度相关理论的准确性也由Eric Heitz在《Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs》中证明[4]。
2014年之前,Disney在SIGGRAPH2012上提出的GSF参考了[Walter 2007]的近似方法,使用Smith GGX导出的G项,并将粗糙度参数进行重映射以减少光泽表面的极端增益,即将α 从[0,1]重映射到[0.5, 1],α的值为 $(0.5+roughness/2)^2$ 。从而使几何项的粗糙度变化更加平滑,更便于美术人员的使用。
UE4在SIGGRAPH 2013上公布的方案为基于Schlick近似,将k映射为 k=a/2 ,去匹配GGX Smith方程,并采用了Disney对粗糙度的重映射$(0.5+roughness/2)^2$:
$$ G_1 (v)=(n·v)/((n·v)(1-k)+k) $$
$$ G(l,v,h)=G_1 (l) G_1 (v) $$
其中,G_1 (l) G_1 (v) 是因为我们需要将观察方向(几何遮蔽Geometry Obstruction)和光线方向向量(几何阴影Geometry Shadowing)都考虑进去。
而在2014年之后,UE4、Frostbite和Unity等引擎都受到Heitz的启发,为了得到更精确的几何遮挡关系,开始考虑入射阴影和出射遮蔽之间的相关性(不考虑相关性会导致计算出的阴影偏多),并在后续更新中各自转向了Smith联合遮蔽阴影函数(The Smith Joint Masking-Shadowing Function)的高度相关遮蔽阴影形式(Height-Correlated Masking and Shadowing),并相应地都做了一些近似与优化。
F: 菲涅尔函数(Fresnel Function)
菲涅尔效应(Fresnel effect)表示的是看到的光线的反射率与视角相关的现象,由法国物理学家奥古斯丁·菲涅尔率先发现:当垂直观察的时候,任何物体或者材质表面都有一个基础反射率F_0(Base Reflectivity),但是如果以一定的角度往平面上看的时候所有反光都会变得明显起来。如果从理想的90度视角观察,所有的平面理论上来说都能完全的反射光线。
而菲涅尔方程作为基于物理的渲染理念中的核心理念之一,描述的是光线入射之后,光会部分反射且部分折射,反射的比例就是菲涅尔系数。菲涅尔系数满足:$ 0<=F_r<=1 $
当光线垂直撞击表面时,该光线被反射(Reflected)为镜面反射光的比率被称为$F_0$。而折射(Refracted)到表面中的光量则为$1-F_0$。但需要注意的是,我们在宏观层面看到的菲涅尔效应实际上是微观层面微平面菲涅尔效应的平均值。也就是说,影响菲涅尔效应的关键参数在于每个微平面的法向量和入射光线的角度,而不是宏观平面的法向量和入射光线的角度。
菲涅尔系数可以由麦克斯韦方程组直接推导出来的,已知平面处两种介质的折射率分别为:$\eta_i、\eta_t$,则根据斯涅尔定理可得折射角和入射角的关系:
$\eta_i sin\theta_i = \eta_t sin \theta_t$
根据麦克斯韦方程组计算推导,平行和垂直偏振光的菲涅尔反射公式:
$$ r_{\parallel} = \frac{\eta_t cos \theta_i - \eta_i cos \theta_t}{\eta_t cos \theta_i + \eta_i cos \theta_t} $$
$$ r_{\perp} = \frac{\eta_i cos \theta_i - \eta_t cos \theta_t}{\eta_i cos \theta_i + \eta_t cos \theta_t} $$
$$ F_r = \frac{1}{2} (r_{\parallel}^2 + r_{\perp}^2) $$

上面这部分参考了:https://zhuanlan.zhihu.com/p/158025828
菲涅尔项的常见模型:
- Cook-Torrance[1982]
- Schlick[1994]
- Gotanta [2014]。
目前业界在渲染时大多采用Fresel的Schlick近似[3]:
$$ c = \frac{n·v}{a\sqrt{1-(n·v)^2}} $$
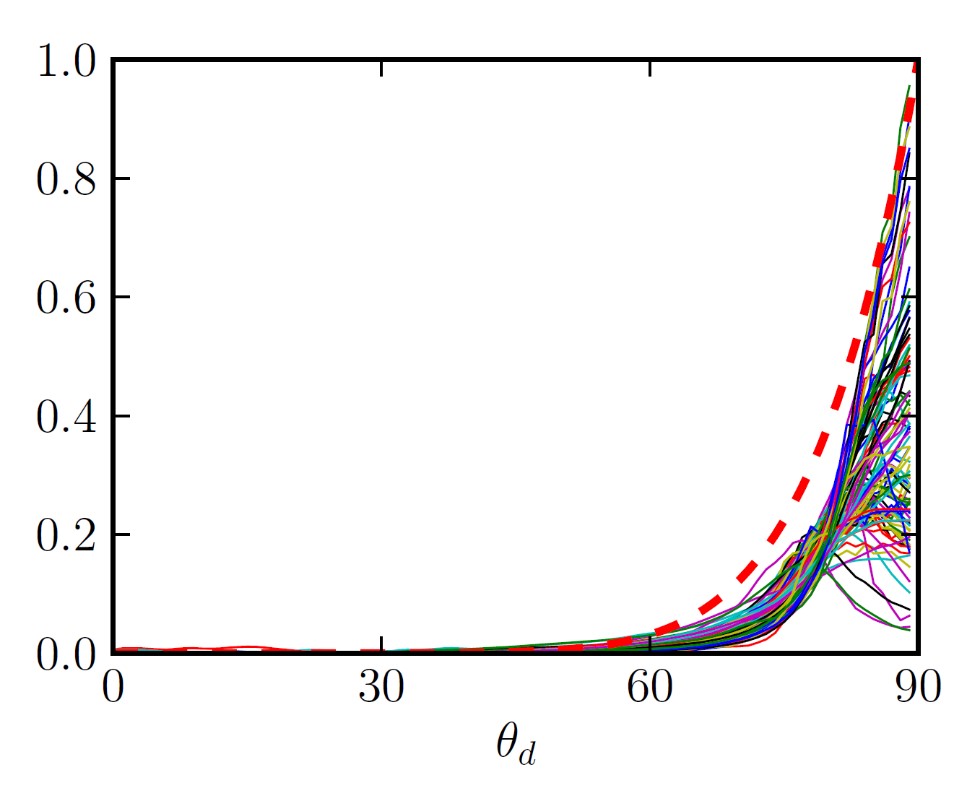
MERL材质[6]中的菲涅尔项如下图,为了方便观察这个曲线经过一定程度的放缩和偏移,在θ_d为90度时都有一定程度的增大。红色虚线部分是理论中的菲涅尔反应。
基础反射率$F_0$的求解方式需要用到材料的折射率:
$$ F_0=(\frac{n_1-n_2}{n_1+n_2})^2 $$
其中,n_1和n_2分别为两种介质的折射率。通常假设 n_1=1 近似于空气的折射率,并用n替换n_2,于是,上式可以简化为:
$$ F_0=(\frac{n-1}{n+1})^2 $$
相对折射率(relative refractive index)
在学习Mitsuba代码的时候,发现其折射率涉及到代码里两个变量:m_eta和m_k,查资料后知道其代表的分别是相对折射率的实部和虚部。
折射率(refractive index)是用来描述光线在某介质内传播速度的比例。对于同一种光源在不同介质中的折射率,如果以真空为基准,就称为相对折射率。而相对折射率通常可以用一个复数来表示: $ n = n’ + k * i $。其中:
- n’是相对折射率的实部,代表光线在该介质中的沿进速度。
- k是相对折射率的虚部,代表光线在该介质中的衰减率。
工业界两种PBR工作流程
Disney Principled BSDF
Reference
- 不同N、G、F的公式可见:https://graphicrants.blogspot.com/2013/08/specular-brdf-reference.html
- B. Burley and W. D. A. Studios. Physically-based shading at disney. In ACM SIGGRAPH, pages 1–7, 2012.










