本文摘自笔者的本科毕业论文,是在学习研究过程中一些对凹凸映射以及粗糙度贴图的知识的整理及个人理解。
凹凸映射及切向空间
凹凸映射(Bump Mapping)是一种通过对纹理贴图采样,扰动模型法线,从而表现出更多像素级别材质细节的技术。在渲染管线中计算片元着色时,三角形面片内部的法线最早是直接通过三个顶点的法线插值得到的。这样的方式保证了模型的平滑,但直接使用插值结果将使得我们无法表达出三角形面片内部的像素级凹凸细节,因此凹凸映射技术应运而生。凹凸映射最早使用的是高度图(Height Map),即通过采样高度图,修改片元的在模型表面的高度,因此模型表面的法线也会改变,从而影响着色,如下图。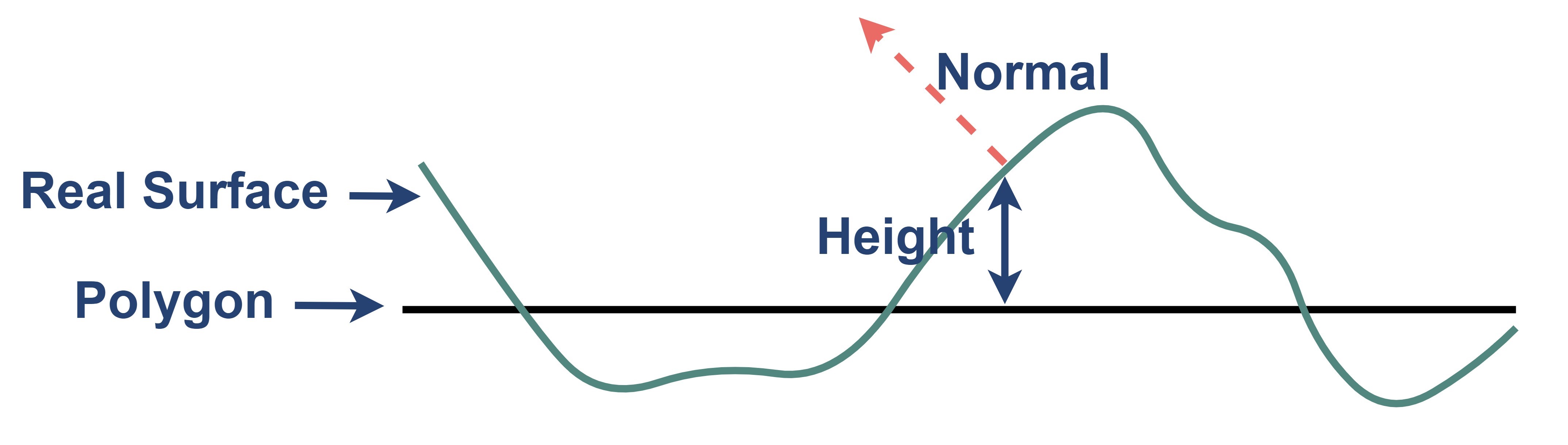
目前行业中广泛使用的基于法线贴图(Normal Map)的Normal Mapping则是基于法线贴图的。法线贴图储存的是模型在切向空间(Tangent Space)的法线信息。切向空间(也可以称为TBN坐标系)是用来解决模型旋转或缩放造成的法线错误问题的。如果法线贴图中储存的是世界坐标下的法线,则模型的旋转和缩放等操作都会导致法线贴图错误,而切向空间可以保证法线不受模型这些变换干扰。切向空间中的Z轴取自顶点法线插值后得到的法线方向。另外两个轴则分别是模型切面上的切线方向(Tangent)和副切线方向(Bitangent),其中切线方向是模型的UV坐标中U分量增长的方向,而副切线方向则是V分量增长的方向。而法线贴图储存的数据就是该处法线相对于从顶点法线插值得到的法线的偏移量(在切向空间下),向量<0,0,1>代表直接使用插值得到的法线而不进行修改。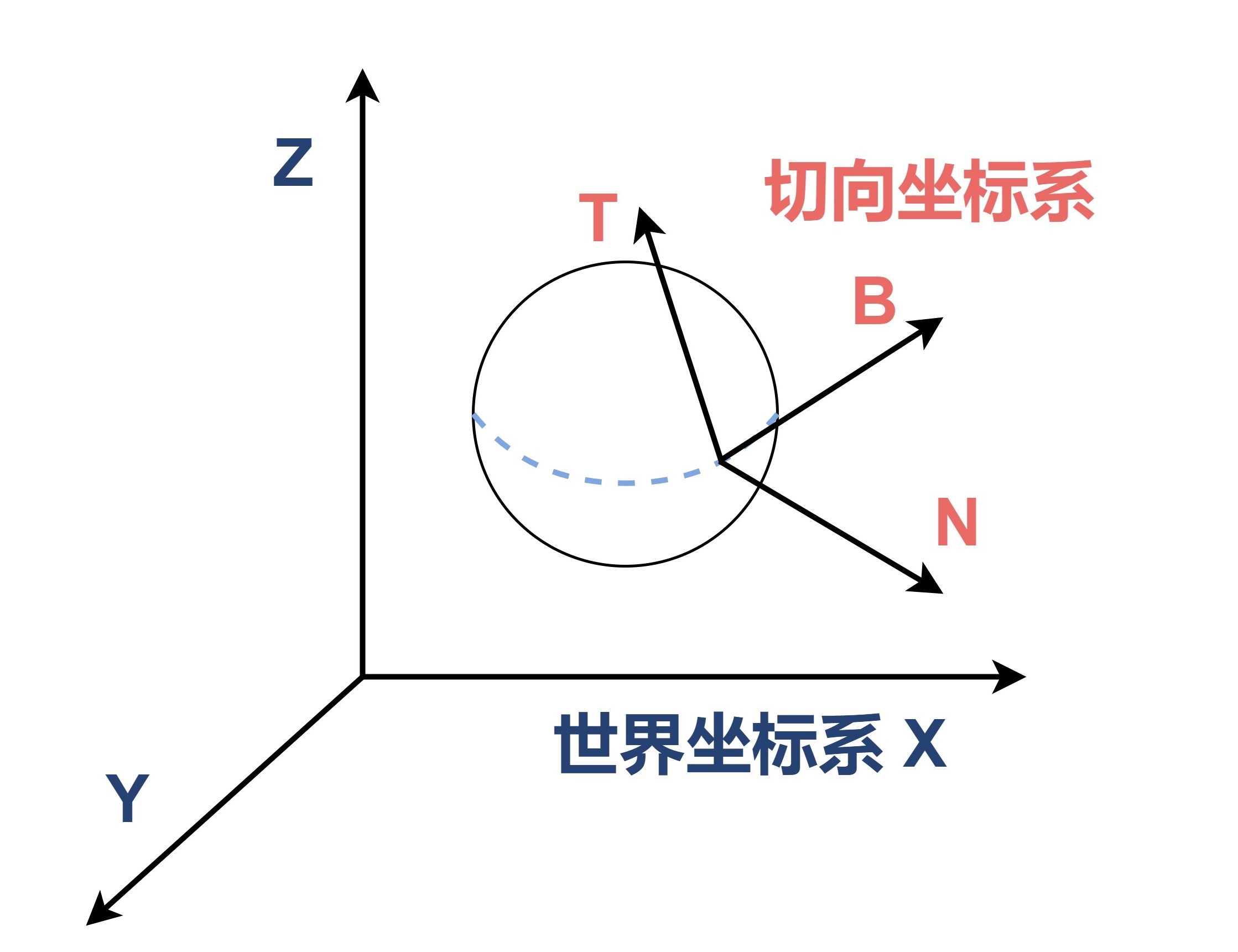
使用高度贴图提取法线的算法实现
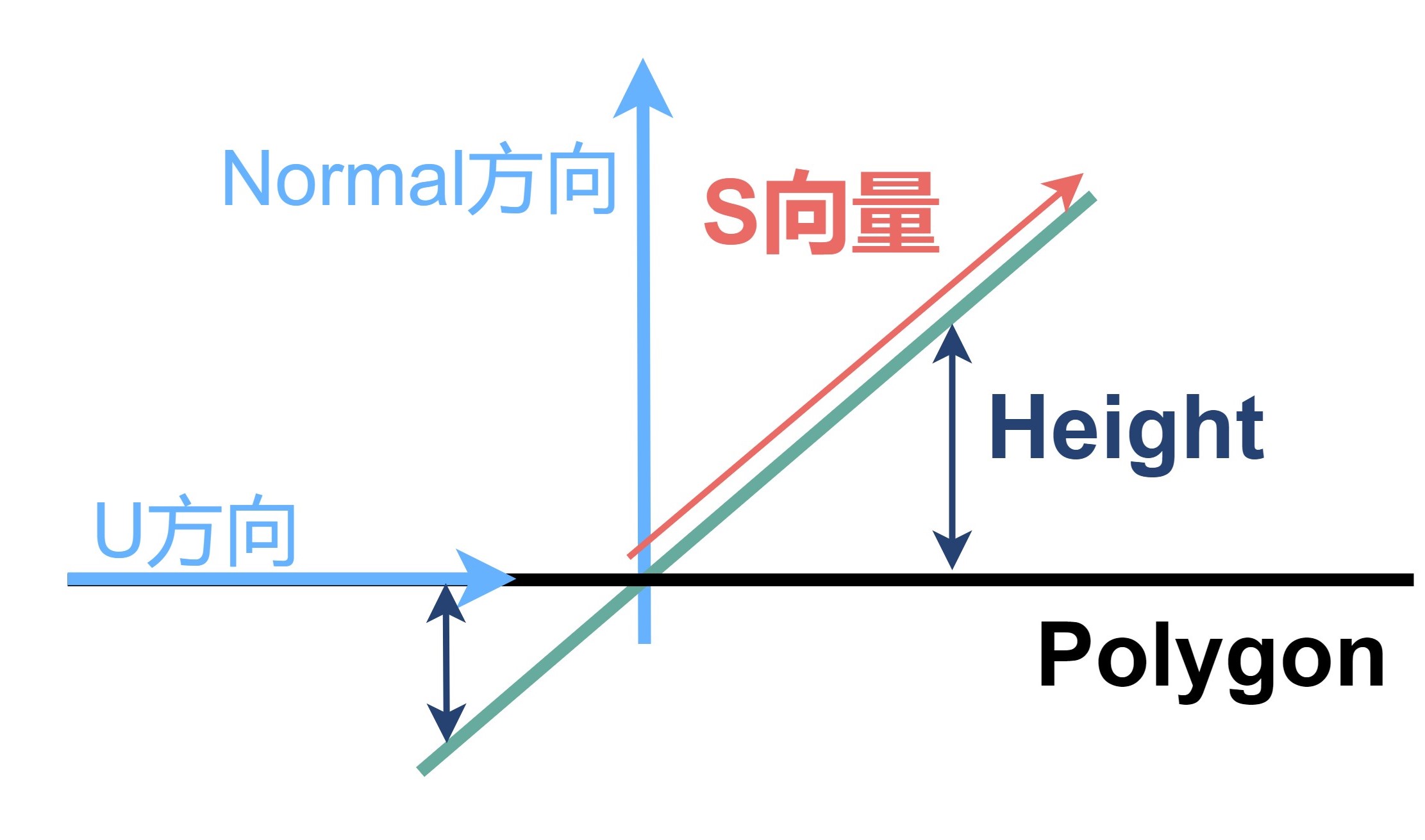
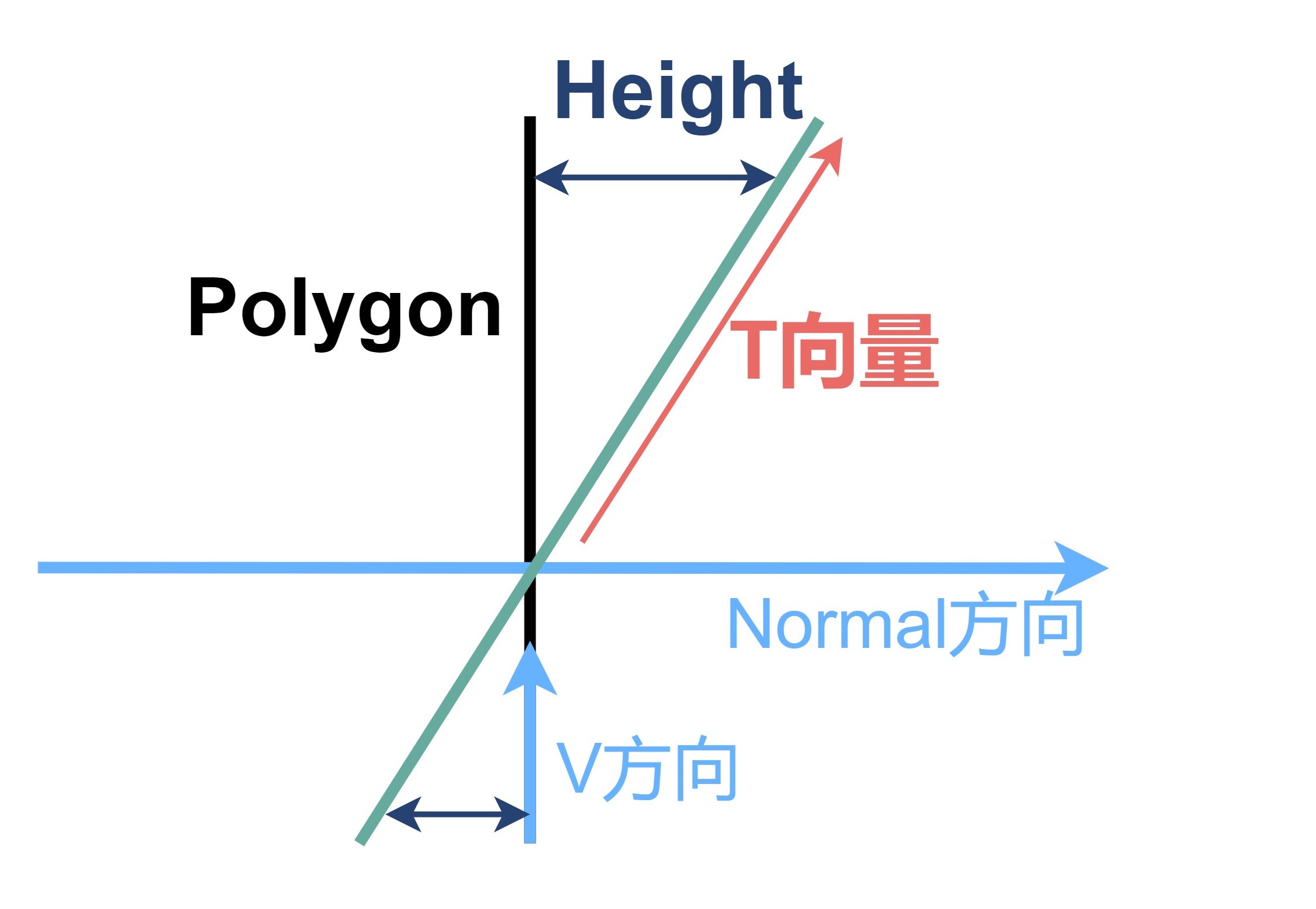
Normal Map其实就是高度场的归一化梯度,因此我们可以使用Lengyel在《Mathematics for 3D Game Programming and Computer Graphics》中提到的思路:通过求解高度图梯度,在切空间构造S向量和T向量,并将其叉乘来得到法线。当沿着U和V方向高度差都为零时,模型没有高度变化,此时法线为Normal(i,j)= <0,0,1>,直接使用插值得到的法线而不对其进行修改。否则,法线就会朝U或者V方向偏移。
设H(i,j)为高度图上(i,j)处像素的高度值,则S和T向量可以表示为:
$$ S(i,j)= <1,0,aH(i+1,j)-aH(i-1,j)> $$
$$ T(i,j)= <0,1,aH(i,j+1)-aH(i,j-1)> $$
其中,a是一个用于放缩的控制参数,其取值取决于高度图的量纲,aH(i+1,j)-aH(i-1,j)表示模型表面沿着U方向的高度差,aH(i,j+1)-aH(i,j-1)表示模型表面沿着V方向的高度差。我们使用S_z和T_z来表示两个向量的Z分量,经过推导可以得到:
$$ Normal(i,j)= \frac{S(i,j)×T(i,j)}{||S(i,j)×T(i,j)||} = \frac{<-S_z,-T_z,1>}{√S_z^2+T_z^2+1} $$
通过测试比较不同方法的效果,在实践中笔者最终使用了Sobel算子,对图像进行滤波以计算图像梯度。Sobel_x和Sobel_y两个算子分别用于计算图像沿着x和y两个方向的梯度,整体梯度G可由x方向的梯度G_x和y方向的梯度G_y按以下公式求得:
$$ sobel_x = \begin{bmatrix} 1 \ 2 \ 1 \end{bmatrix} * \begin{bmatrix} 1 & 0 &-1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & -1 \ 2 & 0 & -2 \ 1 & 0 & -1 \end{bmatrix}$$
$$ sobel_y = \begin{bmatrix} 1 & 2 & 1 \end{bmatrix} * \begin{bmatrix} 1 \ 0 \ -1 \end{bmatrix} = \begin{bmatrix} 1 & 2 & 1 \ 0 & 0 & 0 \ -1 & -2 & -1 \end{bmatrix}$$
$$ G = \sqrt{G_x^2 + G_y^2} $$
Roughness 贴图的物理意义
所有的PBR技术都基于微平面理论。这项理论认为,达到微观尺度之后任何平面都可以使用被称为微平面(Microfacets)的细小镜面来进行描绘。Roughness贴图主要控制表面的粗糙程度,根据平面粗糙程度的不同,这些细小镜面的朝向会有不同程度的随机。理论上来讲,微表面可以通过几何上的变换进行模拟,但是由于这些微平面尺度太小,渲染时已经无法在像素水平对其进行区分,因此PBR理论中引入了粗糙度(Roughness),并通过统计学的方法来近似这些微平面。Roughness越低表示微表面法线分布越统一,反射光线表现更加趋近于镜面反射,而Roughness越高,则表示表面法线分布越混乱越随机,反射光线表现更趋近于漫反射。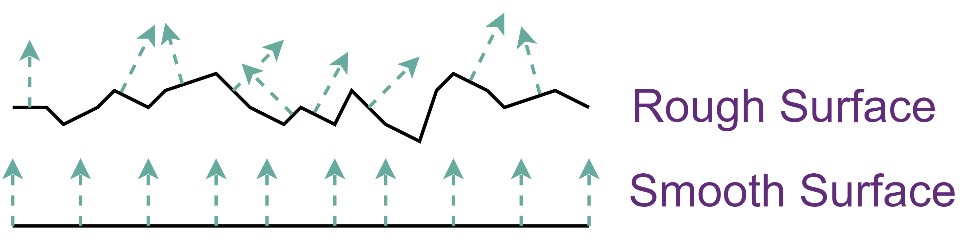
具体到反射方程中,Roughness会影响到BRDF中的D(法线分布函数)和G(几何函数)的计算。
法线分布函数(NDF)被用来描述表面一点内微表面的法向分布。输入一个方向h,法线分布函数会返回法向是h的微平面占所有微表面的比例。法线分布函数有许多不同的模型,但都需要Roughness参与计算,其中目前最常使用的是由Bruce Walter和Kenneth Torrance提出的GGX-NDF,其中,Burley推荐以 α=roughness^2,其中roughness∈[0,1] 的方式代入模型表面粗糙度数据,以让分布以更线性的方式变化:
$$ NDF_{GGXTR} (n,h,α)=\frac{α^2}{\pi((n·h)^2·(α^2-1)+1)^2} $$
几何函数(GSF)则是用于描述由于微面的自阴影行为而导致的光衰减的函数。几何函数模拟了在给定点微面相互遮挡或光在多个微面上反弹的概率,在这些情况下,光在到达视点之前会失去能量,因此宏观上也就表现为我们观察到该处的反射强度会降低。BRDF中使用的几何函数一般指的是包含了在光照方向L上的阴影函数(shadowing function)和在观察方向V上的遮蔽函数(masking function)的联合遮蔽阴影函数。几何函数对于BRDF能量守恒至关重要,BRDF方程一个关键部分是有效表面积(指的是能将光线从光源方向反射到视点方向的表面所覆盖的面积与微面表面的总表面积之间的比率)。而如果不考虑几何函数,则该有效表面积可能会超过总面积,也就破坏了能量守恒。为了准确地生成GSF,大多数拟合公式需要对粗糙度进行采样以确定微平面分布,因此几何函数也与粗糙度Roughness有密切的联系。
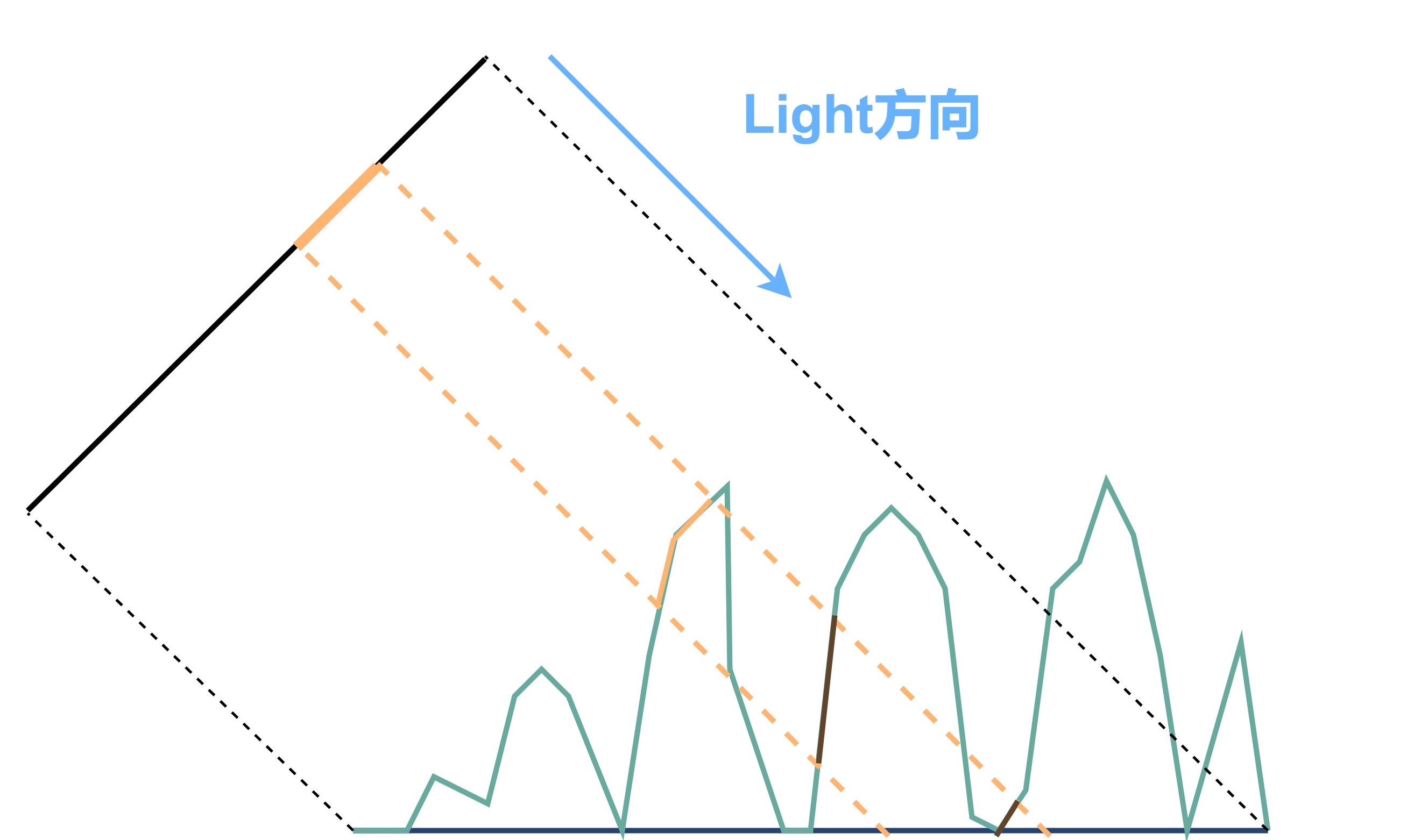
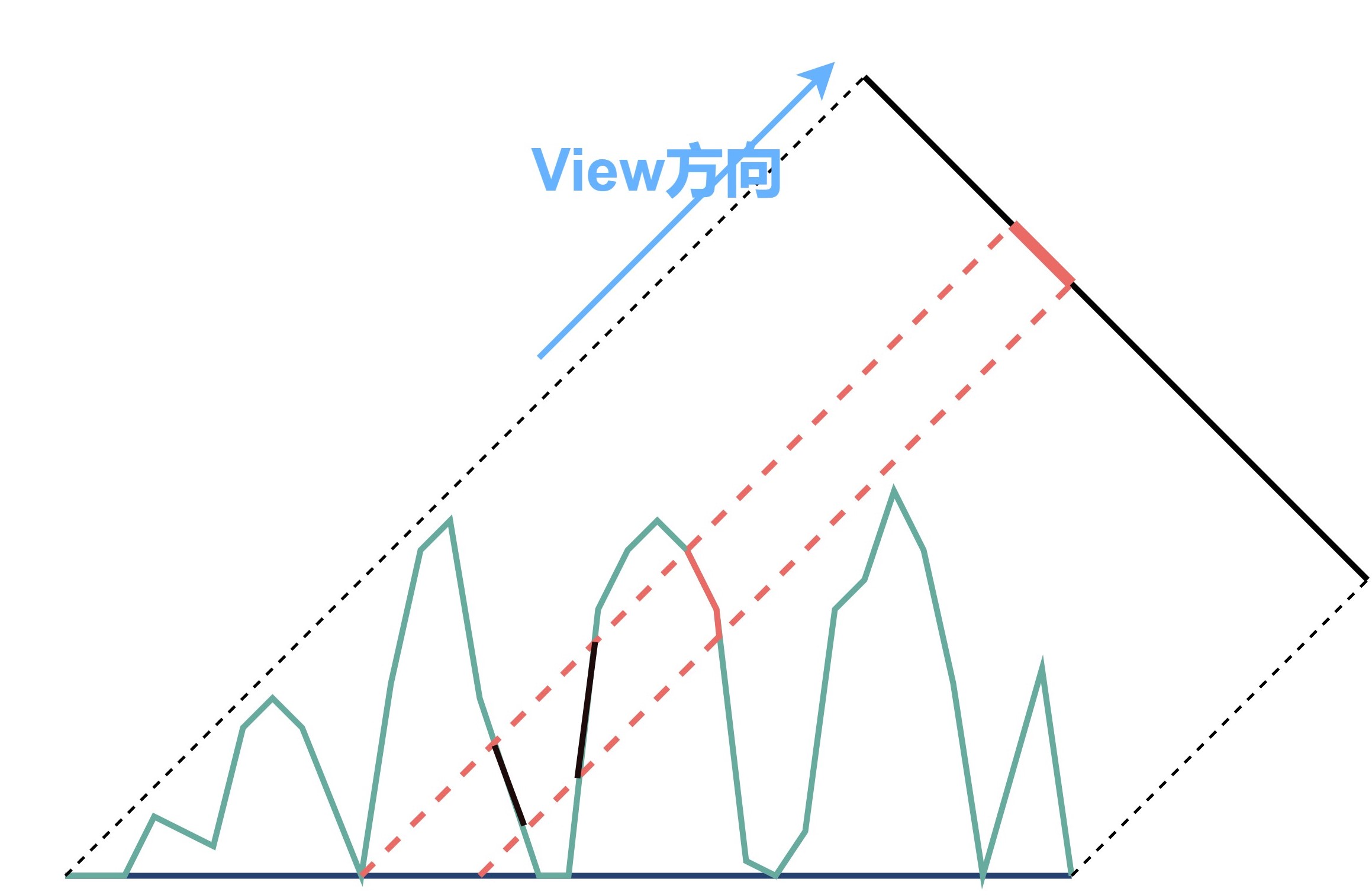
Mipmap技术及其引入的高光走样问题简介
为了避免高光走样问题,现代渲染通常会使用Mipmap技术,但在渲染中用Mipmap技术处理法线贴图会引入高光走样问题。为了解决该问题,NVIDIA提出了一种基于Mipmap的法线方差估计技术,通过计算法线贴图方差信息,修改材质的粗糙度信息,从而解决高光走样。我的毕业论文中在Blender中近似地实现了该效果,下面将对该问题的产生原因及解决原理做进一步阐述。
Mipmap技术现代渲染中必不可少的一个环节。图形学中使用纹理映射(Texture Mapping)将模型上每个点的颜色信息储存在二维的图像上。这种方式方便了美术工作者对模型着色的修改和控制,但贴图尺度过大或者过小都会引发一些渲染走样。当纹理相对于模型过小时,屏幕空间中多个像素点对应在纹理贴图上的坐标都集中在一个像素附近,如果简单地取最近邻的像素值,会导致渲染结果产生严重的走样。实际渲染中一般使用双线性插值来对坐标附近的像素值做一个混合,但这样得到的效果仍不足以弥补问题。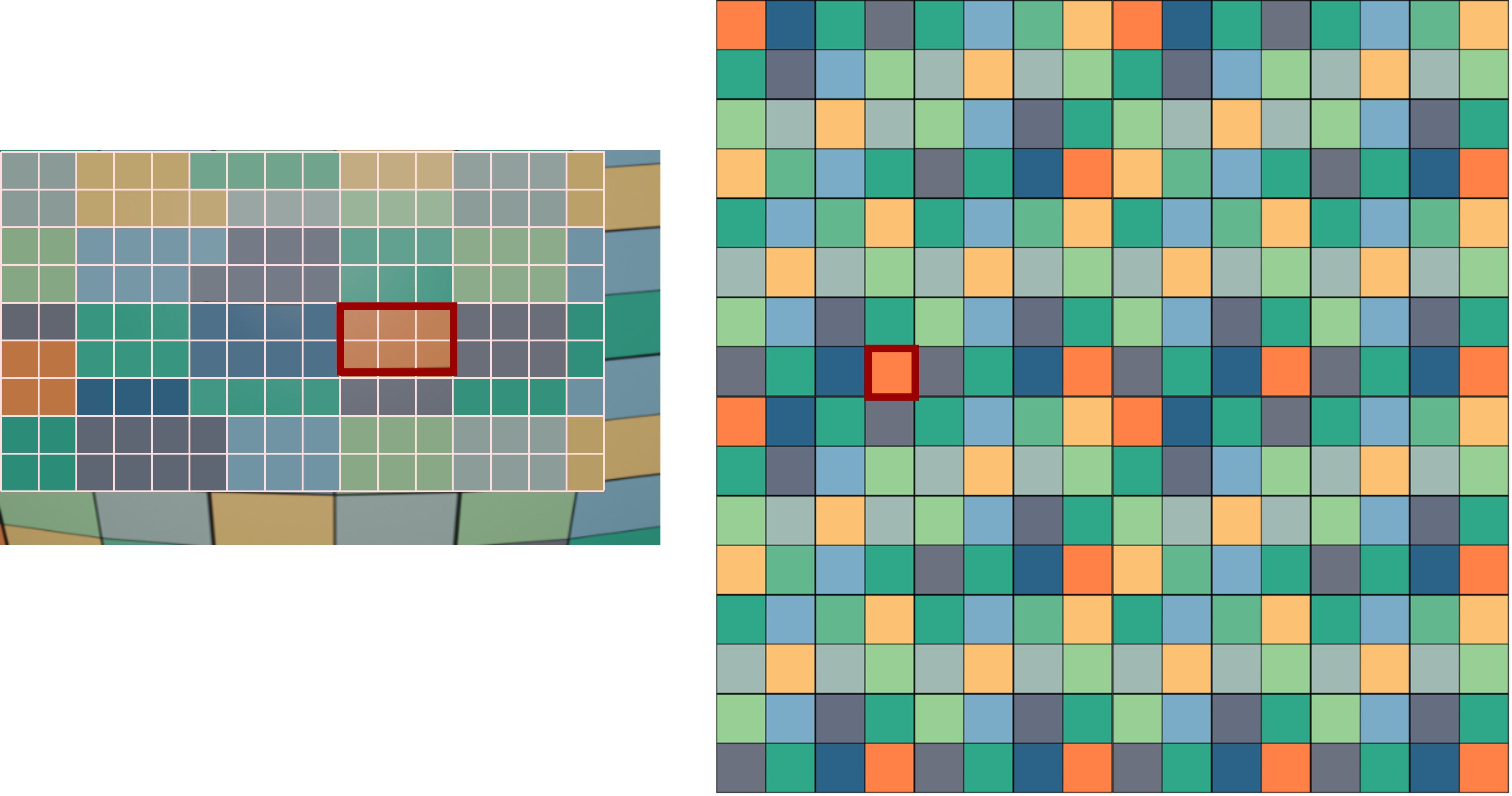

而当纹理相对于模型在屏幕上所占像素数过大时(模型离相机较远时),屏幕空间的一个像素,可能就对应了贴图中一整个区域,这个区域被称为屏幕像素在纹理空间的footprint。此时对于在屏幕空间上相邻的片元来说,如果仅采样贴图上一个点来作为着色值,就会导致屏幕上相邻像素采样得到的颜色是不连续的,从而导致了渲染的锯齿状走样。从信号的角度上来说,这是采样频率过低引起的信息丢失。而使用SuperSampling(超采样)计算量过大,因此Mipmap技术应运而生。
Mipmap技术最早由Lance Williams在他的论文Pyramidal parametrics中提出。Mipmap技术的主要原理就是提前计算像素对应的footprint的均值。具体做法是对贴图进行多次下采样,得到不同尺寸的贴图,在渲染时根据模型与相机的距离,选择不同尺度的贴图。
基于Mipmap的法线方差估计
在Mipmap下采样的过程中,普通颜色贴图中储存的是线性数据,因此可以直接进行线性混合。但法线贴图中储存的是归一化后的方向信息,原理上应该在球面坐标系下做向量插值计算。直接对三个分量线性插值得到的结果会与球面向量插值有所差别。下图给出了二维法线float2(1,0)与float2(0,1)按照从0~1的权重使用两种插值方式得到结果的角度差异(渲染时我们仅关注法线方向)。两种插值结果差异并不大,但使用球面向量插值会大大增加计算量,因此实际渲染管线中通常也直接使用线性插值进行法线贴图的Mipmap。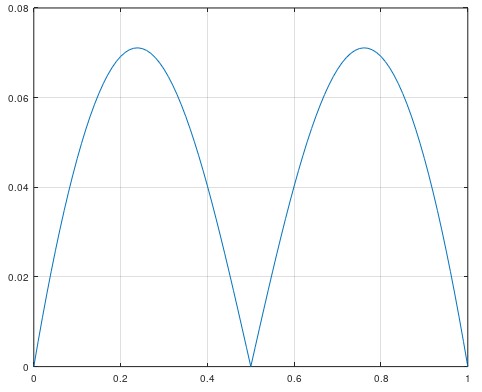
且我们可以得到这样一个规律,如下图,插值后的向量长度越接近一,则插值前两向量夹角越小,反之,则插值前法线夹角越大。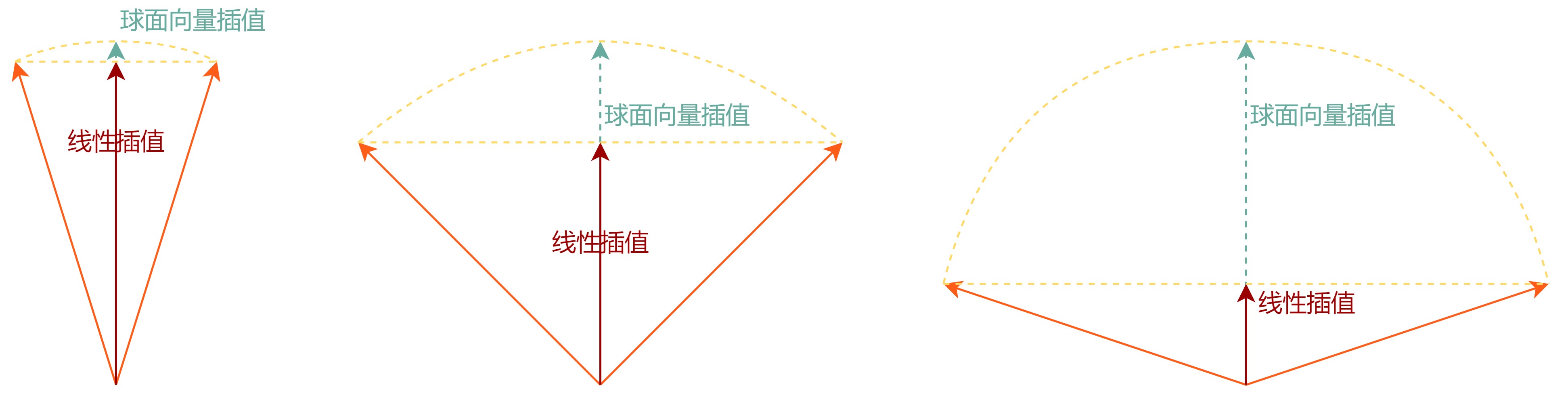
下图提供了向量夹角与线性插值结果长度的关系。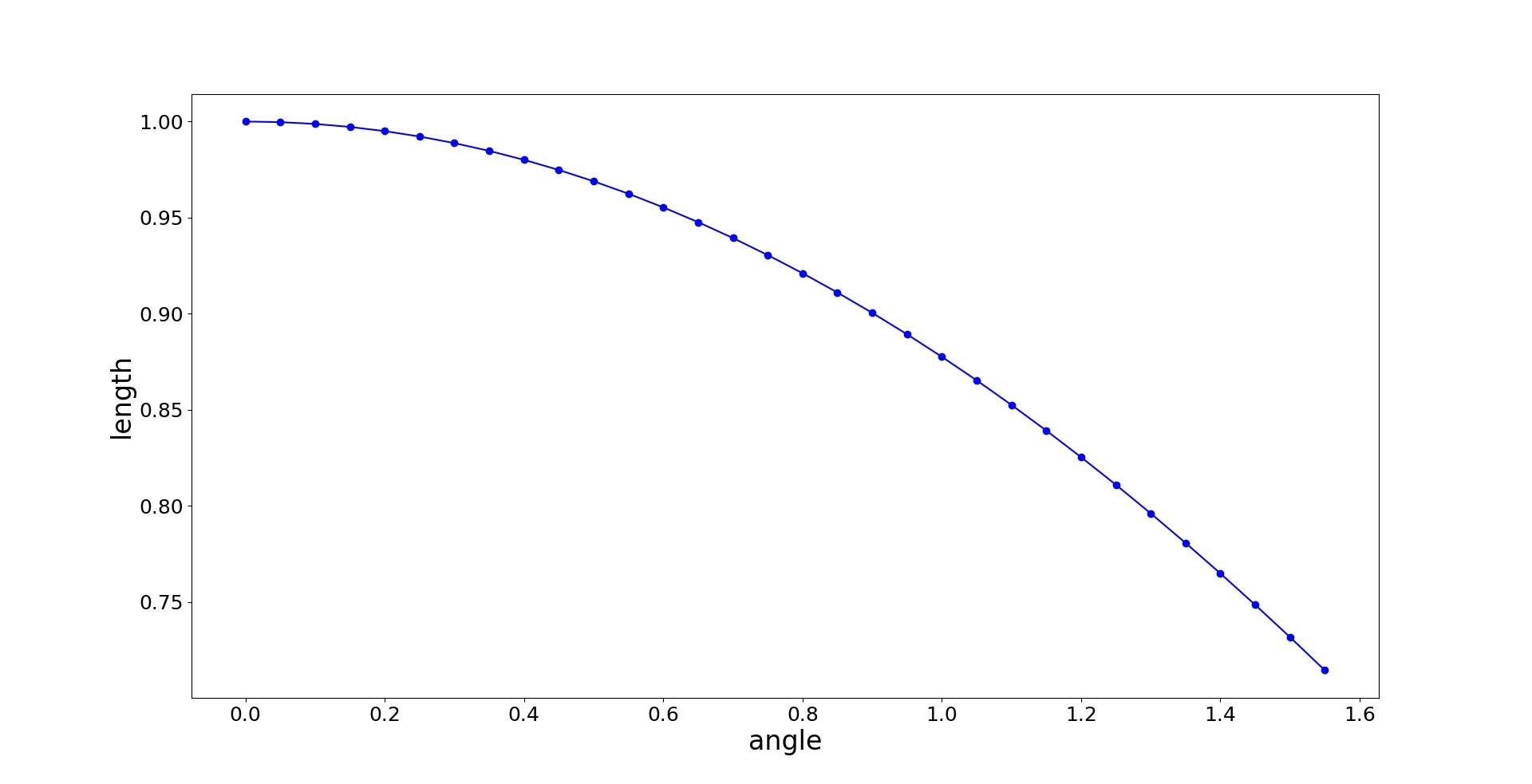
但线性插值得到的Normal结果显然无法完全表达材质的细节,多个法线混合后得到一个法线结果,在这个过程中我们损失了该处混合前法线的变化剧烈程度信息,这部分信息可以用法线贴图的方差来表达。Nvidia借用微表面理论中的原理,假设法线在Mipmap时输入符合高斯分布,标准差为σ。如下图,Nvidia得出了一定范围内的法线标准差与插值后结果的长度关系。其中红色是其实际关系的曲线,而绿色是Nvidia对其的逼近,逼近公式如下:
$$ |N_a | = \frac{1}{1+σ^2} ⇔σ^2 = \frac{1-|N_a |}{|N_a | } $$
因此,只需要采样Mipmap之后的法线贴图,我们就可以使用上述公式估计法线的局部方差。
使用Roughness变化矫正法线Mipmap带来的高光走样及其理解
在实践中我们发现,仅对法线贴图Mipmap仍然会带来高光走样问题,这是由于Mipmap后的法线贴图不能完全表达出之前的材质信息,Mipmap后的贴图只能采样到一个方向信息,却忽略了材质局部的法线变化程度。
我们之所以在渲染中引入Roughness贴图,正是因为无法描述亚像素级别的微平面法线差异。因此从本质上来说,Roughness贴图储存的也是模型的一部分法线信息。而使用法线贴图来宏观表现还是使用粗糙度贴图来微观表现,其分界就在像素级别。一个像素仅可以对应一个法线方向,因此,所有在一个像素内的法线变化信息(不论其对应纹理空间多大的范围),都应该被包含在粗糙度贴图中。也就是说,当法线贴图生成Mipmap时,部分法线信息退化为表面粗糙度信息,我们需要提高模型的粗糙度以避免高光走样问题(如下图)。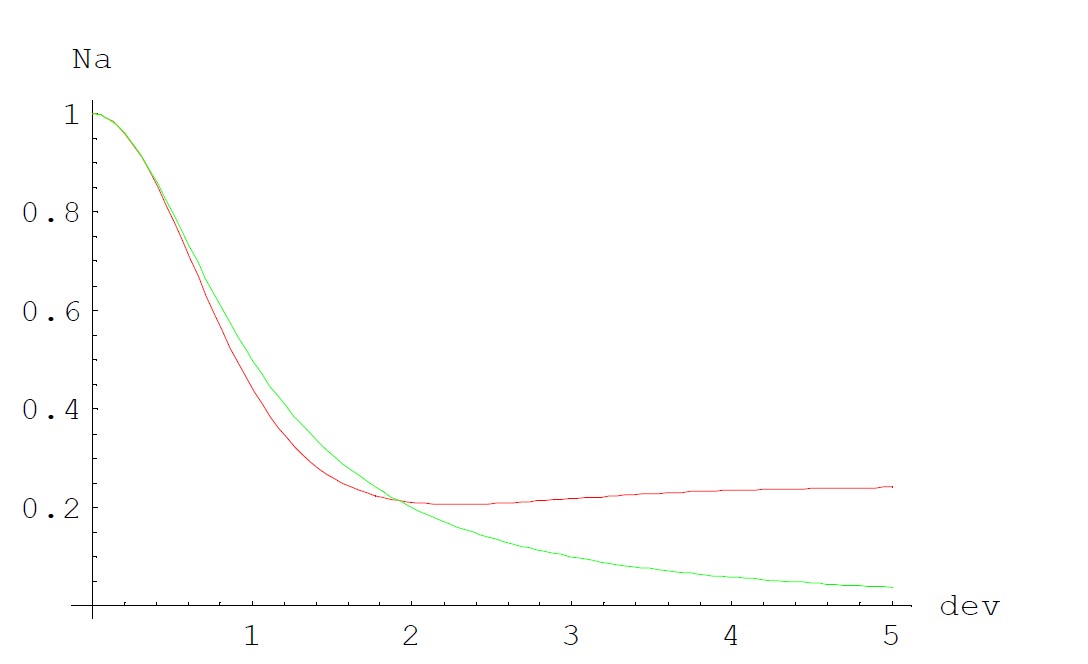
在实践中,笔者将法线贴图的局部方差对应到材质粗糙度的改变,并借鉴了Nvidia提出的方法,通过对Mipmap之后的法线贴图采样,计算法线局部的方差,从而实时地实现了对人脸粗糙度的改变,避免了Mipmap带来的高光走样问题。










